ПРОБЛЕМЫ МОДЕЛИРОВАНИЯ ФЕРМЕНТАТИВНОЙ РЕАКЦИИ

ЭЛЕКТРИЧЕСКИМИ ЦЕПЯМИ

Бирюк Н.Д., Ковалева Т.А., Юргелас В.В.

(Воронеж)

Ферментативная реакция в небольшом сосуде может быть представлена нелинейной системой конечного числа обыкновенных дифференциальных уравнений первого порядка. Число уравнений равно числу исходных компонент, участвующих в реакции. Фермент ускоряет реакцию, уменьшает время ее перехода к своему стационарному состоянию. Если реакция достаточно близка к этому состоянию, то она приближенно представляется системой дифференциальных уравнений с постоянными коэффициентами. Такими же уравнениями описываются радиоцепи с сосредоточенными, постоянными параметрами. Управляемые свободные процессы в таких цепях являются моделями реакций вблизи стационарных состояний.

В современной биофизике [1, 2] активно используются достижения радиоэлектроники. Широко используется, например, понятие динамической модели биологического процесса. Эти динамические модели весьма похожи на нелинейные радиоцепи. Применяются также понятия биологического триггера, биологического автогенератора. Биохимическая реакция в длинном и узком сосуде распространяется вдоль длины сосуда волнами и описывается дифференциальными уравнениями в частных производных, аналогичными телеграфным уравнениям длинной линии. Математическое моделирование в биофизике широко используется. Однако математическим моделям в силу их абстрактности присущи известные ограничения, от которых свободны радиофизические модели. Последние позволяют с помощью приборов (осциллографов, самописцев) визуализировать некоторые скрытые особенности реакций.

Рассмотрим типичную ферментативную реакцию. Пусть в ней принимают участие компоненты, концентрации которых обозначим через . Поскольку каждая компонента вступает в реакцию со всеми или некоторыми другими компонентами, то ее концентрация изменяется во времени:. Наиболее распространенный случай протекания реакции в небольшом сосуде описывается нелинейной системой обыкновенных дифференциальных уравнений первого порядка:

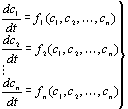(1)

Обычно [1] эту систему поясняют следующим образом: реакция стремится к своему стационарному состоянию, в котором , при этом в результате уже состоявшейся реакции останутся некоторые, заранее неизвестные концентрации . Такое толкование часто бывает неудобным, поскольку заранее неизвестно то состояние, к которому стремится реакция. Во избежание этого проведем математическое преобразование.

В результате замены переменных получится уравнение типа (1), но в новых переменных, являющихся превышениями текущих концентраций над стационарными. Если реакция близка к стационарному состоянию, то все функции можно разложить в ряд Тейлора и отбросить слагаемые высших порядков. Тогда вместо системы типа (1) получим:

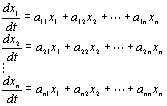(2)

Это типичная система уравнений для свободных процессов радиоцепей с сосредоточенными, постоянными параметрами, которую можно представить, как одно векторное дифференциальное уравнение первого порядка в компактном виде:

(3)
где – неизвестный вектор-столбец -го порядка , – квадратная матрица -го порядка. Элементы вектора являются аналогами компонент реакции, выражаемых количественно как превышения их текущих компонент над стационарными.

Уравнение (3) описывает свободные колебания системы, под которой в данном случае понимается радиоцепь. Для его решения принципиальное значение имеет отыскание корней характеристического уравнения:

(4)
где – единичная матрица -го порядка. Здесь целесообразно выделить следующие три случая: а) все корни уравнения (4) действительны и различны, т.е. ; б) все корни различны, но среди них есть одна или несколько пар комплексно сопряженных, например, , где ; в) среди корней есть один или несколько кратных, при этом сумма числа различных корней с учетом кратности (корень учитывается столько раз, какова его кратность) равна .

В случае а) каждому корню соответствует решение:

или в векторном виде:

(5)
где ,

Для отыскания представим (5) в (3), после элементарных преобразований получим:

(6)
или в развернутом виде:

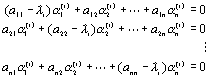
Эта однородная система линейных алгебраических уравнений имеет ненулевое решение, поскольку ее определитель равен нулю, согласно (4). Чтобы решить эту систему, нужно предположить какое-нибудь из произвольным (например, ). После этого одно из уравнений нужно убрать, тогда остальные будут независимыми. Например, удаляем последнее, и его можно использовать для контроля решений. В остальных уравнениях все члены с переносятся вправо. Получается неоднородная система алгебраических уравнений с ненулевым определителем. Она имеет единственное решение. В результате все будут выражены через . Точно так же находятся решения, соответствующие другим корням характеристического уравнения. Их линейная комбинация является общим решением уравнения (3), т.е.

(7)
где – произвольные постоянные.

Нетрудно видеть, что эти константы однозначно определяются из начальных условий. Действительно, полагая , получим:

(8)

Это неоднородная алгебраическая система относительно с ненулевым определителем.

В данном случае константы интегрирования находятся через начальные условия достаточно просто. В других частных случаях могут возникнуть трудности, поэтому целесообразно привести общие рекомендации по отысканию констант.

Пусть дано векторное уравнение (3) и его общее решение:

.

Найдем производную по времени этого равенства с использованием (3):

.

Пусть при задан начальный вектор-столбец . Этого достаточно для определения произвольных констант, для чего в нашем распоряжении есть два приведенных выше векторных равенства, которые при примут вид:

Для вычисления констант достаточно либо первого равенства, либо второго, либо сочетания нескольких уравнений из первого и второго равенств.

В случае б) система допускает комплекснозначные решения, которые обычно в реальных задачах (в том числе и в нашей) не реализуются. Для таких решений нужно задать комплексные начальные условия, что в практических задачах может случится лишь как исключение. Однако оказывается, что пара комплекснозначных решений, построенных на двух комплексно сопряженных корнях характеристического уравнения, может быть преобразована в пару действительных решений. Таким образом, всегда можно построить фундаментальную систему решений, состоящих только из действительных функций времени.

Пусть характеристическое уравнение (4) имеет пару комплексно сопряженных корней . Как и в предыдущем случае, им соответствуют решения:

Для того, чтобы по ним построить пару действительных решений, достаточно использовать только одно из них, скажем первое. Здесь . Для упрощения обозначений отбросим степени в скобках, т.е. и т.д.

Из теории дифференциальных уравнений, например [3], известно, что если корень характеристического уравнения комплексный, то раздельно на его действительной и мнимой части можно построить два действительных решения исходного уравнения (2). Покажем один из способов такого построения.

Вектор является собственным вектором матрицы уравнения (2):

Из этого уравнения с точностью до произвольного множителя можно найти элементы вектора . Для этого целесообразно задать один из этих элементов, скажем . Тогда все остальные элементы однозначно определяются в виде вполне определенных комплексных чисел: . Тогда, используя формулу Эйлера , решение (9) можно представить в виде:

Действительная и мнимая части этой комплекснозначной вектор-функции есть действительные решения исходного векторного уравнения (2):

Эти решения войдут в решения со своими произвольными множителями и

(10)

В радиоэлектронике принято представлять уравнение свободных колебаний не в форме (10) через косинусы и синусы с нулевыми начальными фазами, а через косинусы с ненулевыми начальными фазами, при этом для каждого элемента вектора будет своя начальная фаза. Для такого представления удобно применять формулу:

,

где

В таком случае в (10) -ый элемент вектора примет вид:

где

.

Случай с) является предельным, вырожденным. Можно ожидать, что на практике он будет встречаться много реже, чем два предыдущих случая а) и б). Пусть корень является -кратным. Тогда он порождает независимых решений:

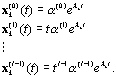
В общее решение эти решения входят с произвольными постоянными:

Рассмотрим ферментативные реакции с двумя и тремя компонентами. Для их моделирования попытаемся использовать известные радиоцепи, широко применяемые в радиоэлектронике. Тем не менее даже для них найти достаточное строгое описание переходных процессов нелегко. Это связано с тем, что радиоэлектроника развивалась под существенным влиянием задач радиосвязи и радиоизмерений, где главную роль играют установившиеся режимы, а не переходные процессы.

Сначала рассмотрим двухкомпонентную ферментативную реакцию, для которой основное уравнение (2) имеет вид:

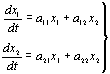(11)

Это – уравнение колебательного контура. В радиоэлектронике обычно подробно анализируется последовательный контур высокой добротности. Такие ограничения для моделирования недопустимы. Возьмем за основу вариант контура, схема которого показана на рис. 1. Это частный случай радиоцепи второго порядка с постоянными параметрами, описываемой системой (11). Общий случай радиоцепи второго порядка в радиоэлектронике не исследован и не может быть изучен с такой полнотой, как последовательный резонансный контур. Представить себе радиоцепь второго порядка общего вида можно, например, так: берем две любые реактивности и сколько угодно активных сопротивлений, из них составляем радиоцепи любой топологии. Таким способом можно получить сколько угодно вариантов радиоцепей второго порядка, кроме тривиальных, вырожденных случаев (отдельные реактивности соединены последовательно или параллельно).

Если в качестве независимых переменных выбрать заряд конденсатора и магнитный поток индуктивности, то уравнение (11) будет конкретизировано так:

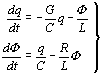(12)

Здесь .

Исключив , получим одно дифференциальное уравнение 2-го порядка относительно заряда:

(13)

Если в (12) исключить заряд, то получится точно такое же уравнение, как и (13), относительно магнитного потока. Это является следствием того, что дуальная цепь по отношению к нашему контуру такая же, как и исходная, т.е. контур является вырожденным по отношению к дуальности. Введем привычные для радиоэлектроники обозначения:

– коэффициент затухания,

– собственная частота,

– параметр сдвига частоты свободных колебаний,

Решение системы (12) представляется по-разному в трех вариантах: 1) , 2) , 3) . Для радиоэлектроники основным вариантом является случай 1), для моделирования – случаи 1) и 2), вариант 3) является граничным, поэтому он имеет меньшее практическое значение, чем остальные.

Рассмотрим случай 1). Решение системы (12) может быть представлено в виде:

(14)
определяются из начальных условий.

Если задать при начальный вектор: то

Если положить , то наш контур вырождается в последовательный контур. Значение проводимости здесь не только количественное, но и качественное. Действительно, для последовательного контура , получается, что чем больше потери, тем меньше частота свободных колебаний. В экспериментах по резонансным методам измерений [4] замечено, что это не так, и приведенная выше формула дает заниженное значение частоты свободных колебаний. В нашем случае , в частности, при имеем . В радиоизмерениях проводимость часто возникает, в ее роли может быть, например, входная проводимость прибора или эквивалентная проводимость неидеального диэлектрика конденсатора.

Рассмотрим случай 2) . Здесь получается два действительных, отрицательных корня характеристического уравнения:

(15)

Свободный процесс является экспоненциально затухающим:

где .

Элементы последних векторов находятся по начальным условиям :

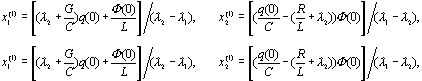
Этот случай может быть применен для моделирования монотонных, неколебательных реакций.

В критическом случае 3) получается один действительный отрицательный двукратный корень:

Как и в предыдущем случае, процесс экспоненциально затухающий, но закон затухания будет другим:

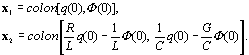
Как видно, свободные процессы в резонансном контуре отличаются достаточным разнообразием, необходимым для моделирования ферментативных реакций разных типов (колебательных, монотонных). Его недостаток заключается в наличии индуктивности, которая в конструктивном отношении является всегда нежелательной.

Рассмотрим цепочку, получающейся из контура (рис. 1) заменой индуктивности на емкость , и емкость переобозначим через . Такая цепочка широко применяется в RC-автогенераторах [5]. Заряды конденсаторов выбираем в качестве независимых переменных, тогда уравнение состояния (11) примет вид:

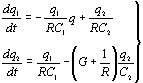(16)

Характеристические корни этой системы оказываются действительными и отрицательными:

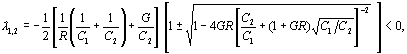
а решение является монотонно затухающим:

Постоянные векторы и однозначно определяются по начальным условиям:

где

Простая цепочка второго порядка обладает ограниченными возможностями для моделирования реакций и может быть применена лишь в таких случаях, когда заранее известно, что реакции монотонные.

Рассмотрим -цепочку 3-го порядка, широко применяемую в -автогенераторах (рис. 2).

Система дифференциальных уравнений этой цепочки относительно зарядов конденсаторов:

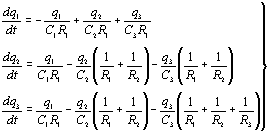(17)

Соответствующее ему характеристическое уравнение является алгебраическим уравнением третьего порядка:

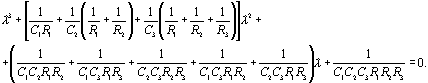
Это уравнение решается в квадратурах. Однако, решение в общем виде связано с громоздкими преобразованиями, а результат получается громоздким и мало прозрачным для осмысления. Поэтому ограничимся частным случаем , , который все же достаточно полно отражает особенности свободных процессов этой цепочки.

Характеристическое уравнение получается достаточно компактным:

Решение этого уравнения [6] приводит к трем действительным отрицательным корням:

Следовательно, общее решение системы (17) является монотонно затухающим. Поэтому моделирующие возможности цепочки ограничены.

Заменим емкость индуктивностью . Система дифференциальных уравнений новой лестничной цепочки следующая:

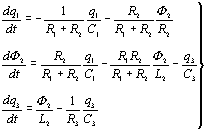
Соответствующее характеристическое уравнение:

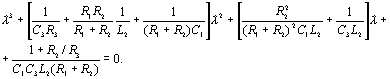
Для уменьшения громоздкости преобразований ограничимся частным случаем . Тогда получим:

(18)

Несмотря на компактность записи, решение этого уравнения громоздко. Покажем, что в зависимости от численных значений элементов цепочки последнее уравнение имеет полный набор решений уравнений этого типа. Представим уравнение в общем виде:

Согласно общепринятому методу решения [6], заменой переменной x=(l+b/3)l получим уравнение:

где

Вид решения зависит от знака дискриминанта :

· если , то одно решение действительно и два комплексно сопряженные;

· если , то все три решения действительны и различны;

· если , то а) при получается одно трехкратное решение, б) при получается два действительные решения, одно из них двукратное.

В нашем случае (18) имеем:

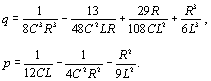
Как видно, р может принимать любые значения как положительные, так и отрицательные. Это значит, что дискриминант уравнения может быть любым.

Фермент в биохимической реакции ускоряет ее, сокращает время достижения стационарного режима. Поэтому в моделях подобных реакций должно быть предусмотрено управление свободными процессами, прежде всего, затуханием. Моделирующие радиоцепи должны включать в себя переменные элементы: емкости, индуктивности, активные сопротивления. В конструктивном отношении легко спроектировать переменное активное сопротивление, труднее – переменную емкость, еще труднее – переменную индуктивность. Поэтому нужно пытаться обойтись потенциометрами и постоянными элементами радиоцепей. В описанных выше простых случаях это удается. Похоже, что и в более сложных случаях можно поступать так же. При теоретическом анализе целесообразно ввести безразмерный параметр управления и соответствующий параметр обозначить через , где – обобщенное обозначение параметра цепи (емкости, индуктивности, активного сопротивления) самый простой случай связан с обозначениями и . Роль фермента в реакциях заключается в изменении параметра управления их моделей.

Радиофизическое моделирование позволяет изучить некоторые особенности ферментативных реакций, которые на прямых экспериментах исследовать невозможно. Задача радиофизического моделирования не является однозначной. Топология соответствующей радиоцепи может быть разной, но число реактивностей в цепи должно быть равно числу компонент реакции. Если реактивности разнородные, то возможности моделирования расширяются, а расчеты при этом усложняются. При моделировании простых реакций есть возможность проводить анализ в общем виде. Однако такой анализ с усложнением реакции становится все более трудным и вскоре невозможным. В случае сложных реакций, по-видимому, основной формой анализа моделей станет приближенное численное исследование с привлечением вычислительных машин.

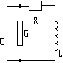
Рис. 1. Колебательный контур как модель двухкомпонентной ферментативной реакции.

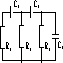
Рис. 2. Лестничная цепочка третьего порядка.

Литература.

1. Рубин А.Б. Биофизика. – Книга 1. Теоретическая биофизика. – М.: Высшая школа, 1987. – 320 с.

2. Рубин А.Б. Биофизика. – Книга 2. Биофизика клеточных процессов. – М.: Высшая школа, 1987. – 304 с.

3. Хартман Ф. Обыкновенные дифференциальные уравнения. – М.: Мир, 1970. – 720 с.

4. Бирюк Н.Д. А.С. № 1128197, GO1h 28/28 // Открытия, изобретения. – М.: ВНИИПИ, 1984. – № 457. – С. 138.

5. Штейн Н.И. Автогенераторы гармонических колебаний. – М.-Л.: Госэнергоиздат, 1961. – 624 с.

6. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. – М.: Наука, 1964. – 608 с.