МОДЕЛИРОВАНИЕ ИЗОМЕРОВ И ХИМИЧЕСКИХ РЕАКЦИЙ

МЕТОДОМ ЗАМЕЩЕНИЙ

Горшков А.Ф.

(Москва)

Развитие теории химического строения, начиная со времен А.М. Бутлерова до наших дней, позволило предсказать существование изомеров, исследовать их сложность и найти пути их синтеза [1, 2, 3, 4]. В данной работе предлагается формализованный подход к построению графовых моделей изомеров при использовании векторов топологии [5], являющихся математическими ограничениями на степени вершин. В качестве математического инструментария предлагается метод замещений [6].

Введем необходимые определения и обозначения.

Вектор подвижных степеней [5] D=(d₁‚d₂‚…‚d_j‚…), где d_j – компонента вектора D, показывающая количество вершин графа, имеющих степень j. Вектор D является неполным, если его некоторые компоненты неизвестны и требуют вычисления.

Вектор закрепленных степеней [5] S=(s₁,s₂,…s_i, …s_n ), где s_i – степень i-ой вершины графа. Для комбинаторных задач вектор D может быть преобразован в вектор S.

L_j,min и L_j,max – соответственно, минимально и максимально допустимые длины цепей, лежащие между корневой вершиной со степенью j и висячей вершиной. Под корневой вершиной понимается вершина с максимальной степенью, если она единственна.

L_1,min и l_1,max – соответственно, минимальная и максимальная длины цепи между висячими вершинами.

L_j,j,max – длина цепи между двумя вершинами с максимальными степенями не менее 3.

Для моделирования структуры молекул типа алканов от C₅ до C₈ данных ограничений достаточно. Для более крупных молекул используются еще некоторые ограничения, которые здесь не рассматриваются.

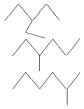
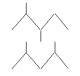
Для иллюстрации метода моделирования рассмотрим построение молекул алкана C₇. Âåêòîð D для линейной структуры молекулы задается тривиально. Поскольку изолированных вершин в молекулярном графе нет, а максимально возможная степень равна 4, то структура вектора будет иметь следующий вид D=(d₁‚d₂‚d₃‚d₄). Для более высоких степеней вершин поступаем следующим образом. Задаем значение интересующей нас степени (номер позиции в векторе D) и число обладающих ими вершин. Допустим, что нас интересуют изомеры, имеющие одну вершину третьей степени. Тогда запишем неполный вектор D=(d₁‚d₂‚1₃‚d₄). Для вычисления остальных компонент неполного вектора воспользуемся следующей теоремой [5].

Теорема. Пусть задан неориентированный граф, тогда параметры n, m искомого подграфа и компоненты вектора D связаны между собой системой диофантовых уравнений S d_ii = 2m‚ S d_i = n.

Таблица 1.

Молекула	Вектор подвижных степеней	Ljmin	Ljmax	l1min	L1max	Lj,j,max	Векторная сложность
	(2,5,0,0)	–	–	5	5	–	0,5
	(3,3,1,0)	L3=2 L3=1 L3=1	L3 = 2 L3 = 3 L3 = 4	4 3 5	4 5 5	– – –	0,83
	(4,1,2,0)	–	–	3 2	3 4	1 2	0,83
	(4,2,0,1)	L4=1 L4=1	L4 = 3 L4 = 2	2 2	4 5	– –	0,83
	(4,0,0,1)	L4=1	L4 = 2	3	3	–	1

Для молекулярного графа алкана C₇ система диофантовых уравнений приобретает следующий вид: d₁+2d₂+3+4d₄ = 12, d₁+d₂+1+d₄ = 7. Решая данную систему диофантовых уравнений, получаем два решения в виде следующих векторов подвижных степеней D=(3,3,1,0) и D=(5,0,1,1). Используя компьютерную программу для решения комбинаторной задачи Бержа [7] на графах с учетом других ограничений (см. табл. 1) получаем структуры изомеров алкана на 2, 3 и 4 строках для первого вектора D и на 8 строке – для второго. Аналогичным образом получаем все остальные векторы D и структуры молекул, представленные таблицей 1.

Векторная сложность молекулярного графа вычисляется по формуле, полученной феноменологически: V=(d_j*j_min + j_max – j_min )/m, при d¹0. При поиске j_max компоненты вектора D просматриваются справа налево до тех пор, пока не встретится компонента, отличная от нуля. При поиске j_min аналогичный просмотр выполняется слева направо. Для графов с однократными ребрами векторная сложность не может превышать 1. Для графов с многократными ребрами 1<V<k+1, где k – максимальная кратность ребер в мультиграфе.

Группа ученых [3] из Свободного Берлинского и Бременского Университетов совершенно справедливо утверждает, что «фундаментальной проблемой физической органической химии является вопрос о механизмах химических реакций». Не меньший интерес эта проблема представляет и для классической органической химии. В данной статье рассматривается один из вариантов формального подхода – использования математического принципа парных замещений [5] для моделирования механизма химических реакций на молекулярных графах.

Рассмотрим формализованную процедуру моделирования на простейшем примере перициклической реакции [3]. В качестве реагентов используем два непредельных углеводорода (рис. 1).

CH₂

//

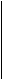
CH CH₂

+ ||

CH CH₂

\\

CH₂

Рис. 1.

Первый этап процедуры сводится к присвоению нумерованных меток атомам углерода в порядке их возрастания и формированию первой части списка ребер молекулярного мультиграфа (см. табл. 2), которое является базовым подмножеством [8]. Каждому ребру мультиграфа присваивается индивидуальный номер как объекту алгоритмической процедуры замещений. При этом физико-химический смысл кратности каждого ребра мультиграфа сводится к валентности свободной (т.е. незанятой водородом) углеродной связи. Вторая часть списка является дополнением первой и включает в себя допустимые валентные связи, которые возможны между двумя и более реагентами. Нумерация второй части списка ребер является продолжением первой. Вторая часть списка может содержать также ребра, относящиеся к реагенту-катализатору, который должен участвовать на промежуточных этапах моделирования химической реакции. Ребра первой части списка являются кандидатами на удаление, а второй – кандидатами на добавление. Следует заметить, что нумерация вершин и ребер в списке имеет значение только для эффективного выполнения алгоритмической процедуры и не имеет физико-химического смысла. Чтобы компоненты катализатора не присутствовали в конечном продукте, имитирующие его дуги должны быть «окрашены» соответствующими кодами.

Таблица 2.

№	Ребро
1 2 3 4 5 6 7	1 – 2 1 – 2 2 – 3 3 – 4 3 – 4 5 – 6 5 – 6
8 9 10 11 12	1 – 5 4 – 6 1 – 4 4 – 5 1 – 6

Второй этап процедуры сводится к преобразованию вектора подвижных степеней в вектор закрепленных степеней [5].

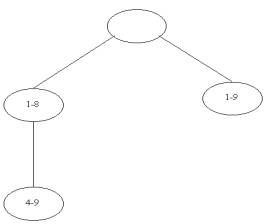
Рис. 2.

Третий этап заключается в построении дерева замещений [6], на верхних ярусах которого формируются узлы с промежуточными результатами моделирования, включая возможные валентные связи с катализатором. В одном или нескольких висячих узлов дерева замещений сформированы молекулярные структуры искомых изомеров. Как промежуточные, так и конечные результаты моделируемой химической реакции могут быть выданы на экран монитора в виде графической картинки.

Пусть структура искомых изомеров, которые должны быть продуктом химической реакции описаны вектором подвижных степеней D=(0,4,2,0). Число компонент связности искомого изомера n=1. Число вершин (углеводородные компоненты) n=6. Число ребер (количество свободных углеродных связей) m=7. Вектор D преобразуется в вектор закрепленных степеней S=(2,2,2,2,3,3). Дерево замещений содержит 4 узла (рис. 2). Промежуточный продукт реакции, полученный на первом ярусе дерева замещений, представляет собой открытую цепь углеводородов CH₂=CH-CH₂-CH₂-CH=CH₂. Â соответствии ñ нумерацией вершин вектор текущих степеней имеет вид S_T=(2,2,3,2,2,3). Поскольку промежуточный результат не удовлетворяет вектору S, то решение продолжено до второго яруса. На рис. 2 узел, в котором синтезирован искомый изомер, отмечен знаком «!». Продукт реакции показан на рис. 1 и представляет собой молекулу циклического углеводорода C₆H₁₀. Векторная сложность первого реагента – 1, второго – 2,5 и продукта реакции – 1,28. Необходимо отметить, что, несмотря на различные механизмы реальных реакций (согласованный и постадийный), моделирование методом замещений выполнялось с помощью одного алгоритма.

Аналогичные простейшие пробные решения (путем ручной прогонки математическим методом замещений) выполнялись при моделировании процесса синтеза этанола. Добавление окрашенных ребер селективного катализатора во вторую часть списка потребовало выполнения двукратной прогонки. Однако суммарное число узлов в дереве замещений при этом уменьшалось по сравнению с вариантом без катализатора. С точки зрения метода замещений это объясняется просто: при наличии катализатора уменьшается деформация начального подграфа, а при отсутствии – увеличивается. Физико-химическое объяснение этому эффекту пока отсутствует. Для получения окончательного вывода требуется выполнить более обстоятельный вычислительный эксперимент с применением вычислительной техники.

Предложенный подход моделирования изомеров и химических реакций, по нашему мнению, имеет не только научно-познавательное значение. При использовании современных мультимедийных технологий появляется возможность создания образовательных компьютерных программ для выполнения «беспробирочных» лабораторных работ, практических занятий и экспериментов, для предсказания возможного существования новых веществ и т.п. Метод замещений, на наш взгляд, целесообразно использовать в качестве алгоритмического ядра в экспертных системах, используемых при проектировании новых технологий синтеза.

Литература.

1. Меррифлд Р., Симмонс Х. Топология конечного точечного множества и молекулярная структура // Химические приложения топологии и теории графов: Пер. с англ. – М.: Мир, 1987. – С. 11-27.

2. Áåðтö Ñ., Õåðíäîí Ó. Подобие в графах и молекулах // Искусственный интеллект: применение в химии. Ïåð. ñ àíãë. – М.: Мир, 1998. – С. 199-206.

3. Хасс Е., Плят П. Многомерная модель. Теоретико-графовый и алгебраический подход к описанию механизмов сложных химических реакций // Химические приложения топологии и теории графов: Пер. с англ. – М.: Мир, 1987. – С. 457-471.

4. Бертц С. Математическая модель молекулярной сложности // Химические приложения топологии и теории графов: Пер. с англ. – М.: Мир, 1987. – С. 236-258.

5. Горшков А.Ф., Соломенцев Ю.М. Применимость реберных замещений в классе комбинаторных задач на графах // ДАН.– 1994. – Т.337 – № 2. – С.151-153.

6. Ãîðøêîâ À.Ô. Об одном методе отыскания экстремальных суграфов // Сиб. Мат. Журнал. – 1985. – Т.XXVI. – ¹1. – C. 44-48.

7. Áåðæ Ê. Теория графов и ее применения. – М.: ИЛ., 1962.

8. Горшков А.Ф. Принцип парных замещений и графовые модели с предписанными степенями вершин // «математика. Компьютер. Образование. – М.: Прогресс-Традиция, 2000. – Вып. 7.