ТЕОРЕТИЧЕСКОЕ ИССЛЕДОВАНИЕ

ЛИГАНД-РЕЦЕПТОРНОГО ВЗАИМОДЕЙСТВИЯ

 

Гуревич К.Г.

 

(Москва)

 

 

Теоретическое исследование взаимодействия лигандов с рецепторами, или лиганд-рецепторного взаимодействия (ЛРВ), является актуальной задачей, т.к. именно в результате ЛРВ может развиваться биологический ответ эфферентной системы (клетки) на эндогенное или же экзогенное воздействие [1, 2]. Кроме того, результаты подобного исследования могут быть использованы для анализа других обратимых бимолекулярных термодинамических реакций, например, фермент-субстрат, антиген-антитело, белок-переносчик–гормон.

Поэтому целью настоящей работы было теоретическое исследование особенностей лиганд-рецепторного взаимодействия.

 

1. Исследование лиганд-рецепторного взаимодействия (ЛРВ) при концентрации лиганда соизмеримой с концентрацией рецепторов.

Наиболее часто ЛРВ описывается в предположении, что концентрация лиганда много больше концентрации рецепторов, т.е. она остается практически постоянной в процессе ЛРВ [1]. Однако, использование радиолигандов с высокой удельной активностью позволяет изучать ЛРВ при концентрации лиганда соизмеримой с концентрацией рецепторов. В этом случае в микроокружении рецепторов наблюдается реальное изменение концентрации лиганда за счет процесса ЛРВ. Поэтому в данной части работы рассматриваются особенности ЛРВ при концентрации лиганда соизмеримой с концентрацией рецепторов.

А) Вывод уравнения, описывающего ЛРВ при концентрации лиганда соизмеримой с концентрацией рецепторов. В простейшем случае лиганд-рецепторное взаимодействие (ЛРВ) описывается при помощи следующей схемы [1, 2]:

,

k+1 и k-1- константы скоростей прямой и обратной реакции, R, L, RL- соответственно молекулы рецептора, лиганда и лиганд-рецепторного комплекса.

Тогда, записав закон сохранения вещества для данной системы, c учетом того, что концентрация свободных молекул рецептора и лиганда представима следующим образом , легко получить:

 

,          (1.1)
где [Ro]- начальная концентрация рецепторов, [Lo]-начальная концентрация лиганда. В стационарных условиях левая часть этого уравнения равна нулю; его корни можно найти по формулам:

 ,

 

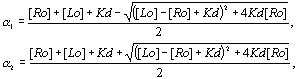
где Kd- константа диссоциации лиганд-рецепторного комплекса.

 

Очевидно, что параметр  равен равновесной концентрации лиганд-рецепторных комплексов при концентрации лиганда, соизмеримой с концентрацией рецепторов. Параметр  в качестве равновесной концентрации лишен физического смысла, так как он может неограниченно возрастать.

Учитывая введенные обозначения, уравнение (1.1) и зная, что в начальный момент времени концентрации лиганд-рецепторных комплексов равна нулю, легко получить:

 

,       (1.2)

где - равновесная концентрация лиганд-рецепторных комплексов.

Б) Редукция уравнения, описывающего ЛРВ при концентрации лиганда соизмеримой с концентрацией рецепторов, при условии, что концентрация лиганда много больше (меньше) концентрации рецепторов. При концентрации лиганда много большей концентрации рецепторов, т.е. когда , уравнение (1.2) сводится к известному уравнению [1]:

 

. (1.3)

При дальнейшем возрастании концентрации добавленного лиганда формула (1.3) легко может быть сведена к следующему уравнению:

 

.   .(1.4)

В отличие от уравнения (1.2), формула (1.3) удобна для вычисления константы скорости ассоциации по следующей формуле [1, 2]:

 

,        (1.5)

где  – угол наклона начальных участков кривой связывания, представленной в полулогарифмических координатах (ln([RL]), t).

 

В) Приближенное решение уравнения, описывающего ЛРВ при концентрации лиганда, соизмеримой с концентрацией рецепторов. Проблема определения кинетических и равновесных параметров в этих условиях. Для того, чтобы получить формулу аналогичную (1.5) для уравнения (1.2), решим исходное дифференциальное уравнение (1.1) не точно, а приблизительно, воспользовавшись тем, что практически любая функция может быть разложена в ряд. Для этого решение дифференциального уравнения (1.1) представим в виде полиномиального экспоненциального ряда:

 

.       (1.6)

Заметим, что выбор ряда (1.6) не случаен и основан на знании аналитического решения дифференциального уравнения (1.1) (формула (1.2)). Для простоты рассмотрим только первые два члена ряда (1.6):

 

.           (1.7)

Учитывая начальные условия, легко получить:

 

.                (1.8)

Тогда константу скорости ассоциации можно оценить по следующей формуле:

 

.        (1.9)

Заметим, что точность аппроксимации формулы (1.2) формулой (1.8) зависит от концентрации лиганда и рецептора, аффинности рецепторов, константы скорости ассоциации. В частности, при концентрации лиганда и рецептора равной 0.1 нМ, аффинности рецепторов 0.1 нМ, константе скорости ассоциации 10+7 мин-1*нМ-1 ошибка аппроксимации уравнения (1.2) уравнением (1.8) не превышает 5%, тогда как в этих же условиях ошибка аппроксимации уравнения (1.2) уравнением (1.3) составляет более 30% [4]. Заметим, что в тех случаях, когда ошибка аппроксимации уравнения (1.2) уравнением (1.8) не удовлетворяет требуемой точности аппроксимации, возможно использование большего числа членов в разложении ряда (1.6). Отметим, что для определения константы скорости ассоциации по формуле (1.9) необходимо вначале определить константу диссоциации лиганд-рецепторных комплексов и концентрацию свободных рецепторов. После этого оценить точность аппроксимации уравнения (1.2) уравнением (1.8). Если она является удовлетворительной, то использовать формулу (1.9), иначе находить более точную аппроксимацию уравнения (1.2).

 

Г) Другой алгоритм определения кинетических параметров. Очевидно, что изложенный выше алгоритм не может быть признан простым. Поэтому в тех случаях, когда нет необходимости определять аналитический вид зависимости [RL](t), может быть рекомендован следующий алгоритм определения искомых параметров. Пусть x(t)- измеренная в эксперименте зависимость концентрации лиганд-рецепторных комплексов от времени, y(t)- вычисленная зависимость концентрации свободного лиганд от времени. Тогда уравнение (1.1) преобразуется следующим образом:

 

.            (1.10)

Т.к. равенство (1.10) должно выполняться при любых значениях времени, то формула (1.10) является переопределенной системой уравнений, содержащей 3 неизвестных параметра (константы скоростей и начальную концентрацию рецептора) и N уравнений, где N- число экспериментальных точек. Поэтому для практического использования формулы (1.10) достаточно потребовать ассимптотического выполнения данного равенства, требуя, например, чтобы разница между суммами квадратов левой и правой частей была минимальной.

После замены коэффициента  на коэффициент  задача (1.10) сводится к задаче линейной регрессии. Можно предположить, что параметры системы (1.10) могут быть определены при помощи методов оптимизации или методов линейной регрессии [3]. Основная проблема при этом: определение . Может быть рекомендовано несколько методов поиска .

Первый метод основан на поиске функции, аппроксимирующей x(t). В качестве аппроксимационной функции может быть рекомендован ряд (1.6) или же следующий ряд типа ряда Де:

 

.              (1.11)

Второй метод основан на поиске не аппроксимирующей, а интреполирующей функции. Данный метод применим лишь когда ошибка определения зависимости x(t) невелика. В качестве интерполирующего метода может быть рекомендован метод сплайн-интерполяции [4], так как он, во-первых, позволяет строить наиболее гладкую интерполяционную функцию, а, во-вторых, коэффициенты сплайн-интерполяции функции x(t) по заданным точкам являются ее производной x’(t) в этих же точках.

Третий метод основан на приблизительном определении x’(t). Наиболее простым и наименее точным приближением производной является ее конечно-разностная оценка [5]:

 

  (1.12)

общее число экспериментальных точек. Данный метод может быть уточнен за счет использования других, более точных, оценок производной.

Четвертый метод основан на переходе от дифференциальной системы уравнений (1.10) к интегральной:

       (1.13)

При этом следует потребовать выполнения условия (1.13) для всех i не равных j, т.е. общее число уравнений в системе (1.13) составит N(N-1)/2 уравнений.

Заметим, что преимущества системы (1.13) перед системой (1.10) очевидны. Левая и правая части этого равенства легко могут быть рассчитаны на основании экспериментальных данных. В настоящее время описано множество методов вычисления определенных интегралов, стоящих в правой части системы (1.13) [5]. Выбор конкретного метода зависит от требуемой точности вычислений и от вида зависимостей  и . Вычисленные определенные интегралы в системе (1.13) могут быть использованы как постоянные величины при вычислении неизвестных коэффициентов ,  и . После замены коэффициента  на коэффициент  задача (1.13) сводится к задаче линейной регрессии.

Отметим, что уравнения (1.10) и (1.13) легко могут быть обобщены на случай кооперативного ЛРВ.

 

2. Вероятностная модель ЛРВ.

Ранее было рассмотрено описание ЛРВ на основании закона сохранения вещества. Однако, с нашей точки зрения, такое описание не позволяет понять механизмы ЛРВ. Поэтому более правильным является описание ЛРВ на основе более общих предположений , например, на основе вероятностных моделей. При этом допускается, что взаимодействие лиганда с рецептором, а также распад лиганд-рецепторных комплексов происходит случайным образом. Вероятностная модель ЛРВ является более общей, чем классическая модель, полученная на основе закона сохранения вещества. Кроме того, вероятностное описание ЛРВ позволяет легко вывести уравнения кинетики конформационных изменений рецепторов в процессе ЛРВ, а так же процессы интернализации, деградации рецепторов, синтеза их de novo и включения вновь синтезированных рецепторов в цитоплазматическую мембрану. Заметим, что вероятностные модели, аналогичные ЛРВ взаимодействию известны в математике. В качестве примера можно привести модели размножения и гибели популяций [6, 7].

А) Вероятностное описание ЛРВ. Рассмотрим случай некооперативного ЛРВ, протекающего при наличии избытка лиганда по отношению к рецепторам. Предположим, что в момент времени  было  молекул свободного рецептора. Также предположим, что за достаточно небольшой промежуток времени  каждая из молекул свободного рецептора с вероятностью  может взаимодействовать с одной молекулой лиганда. За этот же промежуток времени с вероятностью  может распасться одна молекула лиганд-рецепторного комплекса. Если предположить, что за промежуток времени  более сложные процессы не могут произойти и что данные процессы не могут привести к другим процессам, то данная вероятностная модель является простой марковской моделью без последействия.

Если в начальный момент времени было  свободных рецепторов, а в момент времени  –  свободных рецепторов и  лиганд-рецепторных комплексов, то . Тогда вероятность взаимодействия  молекул свободного рецептора с лигандом за время  пропорциональна . Аналогично вероятность распада лиганд-рецепторных комплексов с образованием свободного рецептора пропорциональна .

Обозначим через  вероятность того, что в момент времени  было  молекул свободного рецептора. За промежуток времени   молекул рецептора могут провзаимодействовать с лигандом только в том случае, если в момент времени  было  молекул свободного рецептора. Поэтому вероятность взаимодействия  молекул свободного рецептора с лигандом в момент времени  равна . Аналогично, вероятность образования  молекул свободного рецептора из  молекул лиганд-рецепторного комплекса равна . Вероятность взаимодействия 1 из  свободных рецепторов с лигандом равна  и вероятность распада 1 молекулы лиганд-рецепторного комплекса. если имеется  молекул свободных рецепторов равна . Тогда:

 

     (2.1)

Рассуждая аналогично, для вероятностей  и  будут получены следующие равенства: , .Устремляя  к нулю, получаем следующую систему дифференциальных уравнений:

 

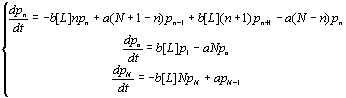            (2.2)

Решение системы (2.2) представляется весьма затруднительным. Однако, в теории вероятностей показано [8, 9], что для описания случайного процесса достаточно рассмотреть производящие функции вероятностей (в нашем случае - число свободных рецепторов является случайной величиной): или производящие функции моментов:  или же производящие функции семиивариантов: . Показано, что процессы, аналогичные процессам гибели и размножения популяций можно охарактеризовать относительно простым уравнением относительно производящей функции моментов [9]:

 

.               (2.3)

В нашем случае число  характеризует процессы взаимодействия лиганда с рецептором. , если образуется молекула свободного рецептора за счет распада лиганд-рецепторного комплекса. , если рецептор взаимодействует с лигандом и число свободных рецепторов уменьшается. В рамках изложенных выше предположений вероятностной модели ЛРВ за промежуток времени  более сложные переходы невозможны. Заметим, что функция  обычно имеет очень простой вид. В нашем случае:  и . Тогда (2.3) переписывается следующим образом:

 

                   (2.4)

В нулевой момент времени число свободных молекул рецептора равно . Поэтому начальные условия для уравнения (2.4) записываются следующим образом: . Тогда задача Коши для производящей функции семиинвариантов запишется следующим образом:

 

           (2.5)

Решим уравнение (2.5) путем разложения производящей функции семиинвариантов и экспонент в ряд Тейлора:

 

    (2.6)

 (2.7)

где - математическое ожидание числа рецепторов, - дисперсия числа рецепторов. Учитывая, что концентрация свободных рецепторов равна начальной концентрации рецепторов минус концентрация лиганд-рецепторных комплексов, очевидно, что формула (2.6) с точностью до обозначений совпадает с формулой (1.4). При этом  соответствует ,  – ,  – . Знак минус в последнем выражении стоит, т.к. параметр  описывает увеличение числа свободных рецепторов, а параметр  – уменьшение числа лиганд-рецепторных комплексов, т.е. эти величины описывают один процесс, но по отношению к различным направлениям. Таким образом, константы скоростей ассоциации и диссоциации могут быть проинтерпретированы как среднестатистические вероятности образования и распада лиганд-рецепторных комплексов. Поэтому закон сохранения вещества может быть проинтерпретирован как вероятностный закон, выполняющийся при больших . Это дает основание для рассмотрения в дальнейшем (часть 3) статистических моделей ЛРВ.

 

Б) Следствия из вероятностной модели ЛРВ. Заметим, что само по себе уравнение (2.6) не интересно, так как повторяет уравнение (1.4). Однако. вероятностные модели ЛРВ позволяют получить ряд интересных следствий. Во-первых, может быть определена дисперсия числа свободных рецепторов и рассчитана макроскопическая энтропия состояния системы. Во-вторых, может быть определен закон распределения числа рецепторов. В-третьих, вероятностные модели позволяют учитывать изменение концентрации рецепторов не только за счет ЛРВ, но и за счет процессов интернализации, деградации рецепторов, синтеза рецепторов de novo и включения вновь синтезированных рецепторов в цитоплазматическую мембрану. В-четвертых, вероятностные модели позволяют легко описывать конформационные изменения рецепторов в процессе ЛРВ.

Не останавливаясь на подробном выводе, отметим, что случайная величина  числа свободных рецепторов имеет сложное распределение Пуассона

 

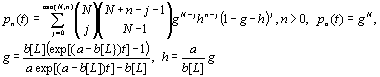       (2.8)

с математическим ожиданием и дисперсией, описываемыми формулами (2.6) и (2.7). Из формулы (2.7) следует, что с течением времени дисперсия случайной величины числа свободных рецепторов стремится к нулю, тогда как при малых значениях времени она может быть весьма существенной. Следовательно, изучение ЛРВ при малом времени ЛРВ представляется весьма проблематичным.

Формула (2.6) позволяет получить еще одно очень интересное следствие. Как известно, из теории пуассоновских законов и цепей Маркова [8], одна экспонента в уравнении для математического ожидания систем аналогичных (2.1) будет лишь при статистической независимости процессов взаимодействия одних молекул рецептора с лигандом от других молекул рецептора. В противном случае, в уравнении (2.6) будет несколько множителей, зависящих от времени ЛРВ. Отметим, что простейшим случаем, приводящим к появлению двух экспонент в уравнении типа (2.6), является кооперативное ЛРВ. При этом после взаимодействия рецептора с одной молекулой лиганда сродство к следующей изменяется. Т.е. данный процесс не является простым марковским, так как имеет последействие. Также предположение о статистической независимости ЛРВ может нарушаться, если в процессе ЛРВ изменяется функциональное состояние клетки, происходит изменение конформации рецепторов, их числа за счет процессов интернализации, десинтезации, синтеза de novo и включения вновь синтезированных рецепторов в цитоплазматическую мембрану. Эти процессы будут рассмотрены ниже.

 

В) Описание процесса изменения концентрации рецепторов за счет ЛРВ, интернализации, деградации рецепторов, синтеза рецепторов de novo и включения вновь синтезированных рецепторов в цитоплазматическую мембрану. До сих пор мы предполагали, что суммарная концентрация рецепторов на цитоплазматической мембране остается постоянной (для внутриклеточных рецепторов: внутриклеточная концентрация). Однако, в общем случае, это не так. С течением времени in vivo и in vitro могут происходить процессы интернализации (транспорта рецепторов с поверхности клетки в цитоплазму), десинтетизации (лизосомальной деградации) рецепторов, синтеза рецепторов de novo и включения вновь синтезированных рецепторов в цитоплазматическую мембрану клетки [10, 11].

Изменение числа рецепторов может быть пропорционально концентрации лиганда и описываться членом , может быть пропорционально числу связанных рецепторов и описываться членом  и может быть спонтанным и описываться членом . Для определенности положим . Тогда:

 

     (2.9)

Решая (2.9), можно получить:

, ,

 

т.е. это- отрицательное биномиальное распределение.

Особый интерес представляет случай, когда . С фармакологической точки зрения этот случай может быть проинтерпретирован как необратимое связывание лиганда с рецептором. Такое взаимодействие может наблюдаться при взаимодействии a-бунгаротоксина из яда кобр с Н-холинорецепторами. Тогда:

 

,

 

т.е. это распределение Пуассона.

Заметим, однако, что появление того или иного распределения ничего не говорит о механизме ЛРВ. В данном примере пуассоновское распределение может быть интерпретировано следующим образом. После необратимого взаимодействия рецепторов с лигандом вероятность того, что число свободных рецепторов мало, велика, тогда как вероятность того, что число свободных рецепторов велико, мала. Этот вывод соответствует действительности.

 

Г) Описание различных конформационных изменений рецептора. Ранее мы предполагали, что все переходы происходят случайным образом независимо друг от друга. Это означает, что промежутки времени, в течении которых рецептор не связан с лигандом, распределены по экспоненциальному закону. Однако, если между взаимодействием лиганда с рецептором есть некоторая зависимость, то данный процесс не является простым марковским без последействия и не описывается распределением Пуассона. Можно предположить, что в процессе ЛРВ рецептор может принимать  конформаций, в которые можно также включить и рецепторы, с которыми происходят процессы интернализации, деградации, синтеза и включения в цитоплазматическую мембрану.

Теория конформационных изменений была предложена Франклиным и Ариенсом [12, 13]. Согласно этой теории процесс ЛРВ описывается следующей схемой:

 

,

 

где:  – молекула лиганда,  – молекула рецептора,  – лиганд-рецепторный комплекс,  – активный рецептор и – неактивный рецептор. Активный и неактивный рецепторы являются конформациями «обычного» рецептора, которые обратимо могут переходить друг в друга.

Пусть - число находящихся в j-той конформации рецепторов. Предполагая для простоты частоты перехода из одной конформации по циклу конформаций 1,2,...,k,1,... пропорциональными концентрации лиганда, а по обратному циклу – независимыми от нее, получаем: , , где - функции, описывающие переходы на j-тую и из j-той конформации,  – вероятности переходов, связанные и несвязанные с концентрацией лиганда. Тогда:

 

 

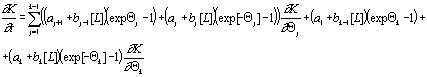
Решим это уравнение методом разложения в ряд. Тогда:

 

,             (2.10)

где - математическое ожидание числа рецепторов j-той конформации, - начальное число рецепторов этой конформации. Если начальное число рецепторов q-той этой конформации равно нулю, то уравнение (2.10) для этой конформации запишется следующим образом:

 

,           (2.11)

где - математическое ожидание времени, когда появится 1 рецептор в q-той конформации. В общем случае вычисление  достаточно сложно. При этом в уравнении (2.11) может возникнуть несколько экспонент, в т.ч. и комплексных. К подобному решению может привести также предположение о более сложной функциональной зависимости между конформационными переходами. Можно предположить, что появление комплексных экспонент в уравнении (2.11) является одним из объяснений так называемого феномена колебаний рецепторного связывания, впервые описанного для клеток нейроглиомы [14, 15].Заметим, что в теории метаболического контроля [16] также выводятся уравнения, описывающие конформационные изменения [фермента]. Однако, уравнения теории метаболического контроля, в отличие от уравнения (2.9), являются стационарными.

 

Литература.

1.     Варфоломеев С.Д., Гуревич К.Г. Биокинетика. – М.: Фаир-пресс, 1999. – 720 с.

2.     Гуревич К.Г.– Биохимия. – 1997. – Т. 62. – № 9. – С. 1121-1124.

3.     Химмельблау Д. Прикладное нелинейное программирование. – М.: Мир, 1975.– 534 с.

4.     Трауб Дж., Вожньяковский Х. Общая теория оптимальных алгоритмов. – М.: Мир, 1983. – 382 с.

5.     Хемминг Р. Численные методы.– М.: Наука, 1972.– 400 с.

6.     Ledermann W., Reuter G.E. – Philosoph. Trasactions Royal Society, London, Ser. A, – 1954. – V. 246. – P. 321-369.

7.     Karvin S., McGregor J. – Proceeding National Academy Sciences USA, 1955. – V.4. – P.387-391.

8.     Феллер. Введение в теорию вероятностей и ее приложения. – М.: Мир, 1967. – Т.1. – 498 с. – Т.2. – 752 с.

9.     Bailey N.T.J. The elements of Stochastic processes. – London, Wiley, 1964.

10.  Gero A. Desintization.– J. Theor. Biol., 1983. – V.103. – P.137-161.

11.  King A.C., Cuatrecasas P. – The New England J. of Medicine, 1981. – V.305. – N.2. – P.77-88.

12.  Franklin T.F. – Biochem. Pharmacol., 1980. – V. 29. – P. 853-856.

13.  Ariеns E.J. – J. Cardiol. Pharmacol., 1983. – V. 5. – N. 1. – P. 8-15

14.  Сухомлин Т.К., Мелихова Е.М., Курочкин И.Н., Варфоломеев С.Д. – Биохимия, 1992. – Т. 52. – № 11. – С.1648-1657.

15.  Sukhomlin T.K., Melikhova E.M., Kurochkin I.N., Varfolomeev S.D. – Biochem. Bioph. Acta, 1992. – V. 1132. – P. 226-228.

16.  Холоденко Б.Н. Стабилизирующая регуляция в полиферментных системах: моделирование биоэнергетических процессов. Автореф. дисс. … д. ф.-м. н. – М., 1988. – 45 с.