Исследования последних лет
убедительно показали, что структура ДНК, открытая Уотсоном и Криком в 1953 году
[1-2], не является статичной. Напротив, молекула ДНК обладает большой
внутренней подвижностью [3-4]. Среди возможных внутренних движений ДНК особый
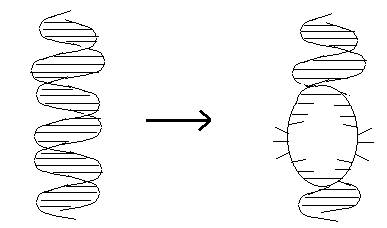
интерес представляет движение, которое называют локальным расплетанием двойной
спирали ДНК (рис. 1). Некоторые авторы называют это движение образованием
открытого состояния, а способность молекулы ДНК образовывать открытые состояния
биологи часто называют способностью ДНК “дышать”.
![]()
![]()
Рис. 1. Локальное расплетание
двойной спирали ДНК.
Почему эти движения интересны?
Ответ заключается в той важной роли, которую играют эти движения в
функционировании молекулы. Действительно, многие исследователи склоняются
сейчас к мнению, что процесс белок-нуклеинового узнавания включает как
необходимый элемент образование открытого состояния, чтобы иметь возможность
“узнать” нужную последовательность оснований. Хорошо известно, что локальное
расплетание двойной спирали является важным элементом первой стадии процесса
транскрипции, во время которой происходит связывание РНК-полимеразы с
промоторной областью ДНК. Образование открытых состояний играет важную роль в
процессах денатурации ДНК.
Как происходит активация этих
движений? Нужно сказать, что существует несколько предположений на этот счет.
Некоторые исследователи полагают, что образование открытых состояний возможно в
результате случайных флюктуаций. Существует мнение, что такие состояния могут
образовываться также в результате столкновения ДНК с “горячими” молекулами
раствора. По-видимому, локальное расплетание двойной спирали может быть
индуцировано воздействием внешних полей. Наконец, оно может быть активировано,
в результате взаимодействия ДНК с белковыми молекулами.
Как эти движения могут быть
описаны математически? Поскольку локальное расплетание двойной спирали ДНК
является движением большой амплитуды, для математического описания такого
движения необходимо привлечь аппарат нелинейной теории. Первая попытка
сконструировать нелинейную математическую была предпринята Инглэндером с
соавторами [5]. Эта модель описывала вращательные движения оснований вокруг
сахаро-фосфатной цепочек ДНК. Если предположить, что вращательные движения
оснований вносят основной вклад в образование открытого состояния, то модель
Инглэндера, улучшенная позднее в работах Йомосы [6], Такено и Хоммы [7],
действительно может рассматриваться как математическая модель расплетания
двойной спирали ДНК. Модель состоит из двух связанных нелинейных уравнений вида
I1 (d2Y1/dt2)
– K1R20 a2 (¶2Y1 /¶z2)
+ kR02 [2 sinY1- sin(Y1
+ Y2)] =0; (1)
I2 (d2Y2/dt2) – K2R20
a2 (¶2Y2/¶z2)
+ kR02 [2 sinY2 – sin(Y1
+ Y2)] =0;
где Y1, Y2
– угловые смещения оснований в первой и второй цепочках ДНК; I1, I2
– моменты инерции оснований; K1, K2 коэффициенты жесткости
первой и второй цепочек; k – коэффициент жесткости водородных цепочек; R0
– радиус ДНК; a – расстояние между парами оснований вдоль основной оси ДНК.
Солитоноподобные решения (кинки и бризеры) интерпретировали в этих и
последующих работах [8-11], как решения, описывающие образование открытых
состояний в ДНК. Эти решения были использованы для объяснения экспериментальных
данных по водородно-тритиевому обмену [5], рассеянию нейтронов [12-13],
эффектам диссипации и влиянию внешних полей [14], функционированию [15-16].
Существует, однако, еще один
важный тип внутренних движений в ДНК, которые вносит существенный вклад в
локальное расплетание двойной спирали. Это поперечные движения оснований.
Пейрард и соавторы [17-18] детально исследовали эти движения и показали их
важную роль в процессах денатурации ДНК. Нелинейная модель, построенная
Пейрардом, состоит их двух связанных уравнений вида
m (d2v1/dt2)
– K [a2 ¶2v1/¶z2]
+ ¶V/¶v1 = 0; (2)
m(d2v2/dt2) – K [a2 ¶2v2/¶z2]
+ ¶V/¶v2 =0;
где V – потенциал Морзе
V = D{exp[-A(v1 –
v2)] – 1}2; (3)
описывающий две или три водородные связи между
основаниями внутри пар; v1, v2 – поперечные смещения
оснований.
Можно ожидать, что точное
описание локального расплетания двойной спирали ДНК должно включать оба типа
движений: вращательные движения оснований и поперечные движения. Таким образом
нелинейная математическая модель должна состоять из четырех нелинейных
математических уравнений: двух для вращательных движений и двух для поперечных
движений. Такие уравнения были получены нами
(m R20)
(d2 f1/dt2) + (m R20) (1
– f1) (dY1/dt)2 =
+ (K R20)
a2 ¶2f1/¶z2
+ (K R20) (a2) (¶Y1/¶z)2(1
– f1) –
- (k R20)
(f1 + f2) + (2k R20) (1
– cosY1) –
- (k R20
) (1 – f1)[1-cos(Y1 + Y2)]
;
(4)
(m R20)
(d2 f2/dt2) + (m R20) (1
– f2) (dY2/dt)2 =
+ (K R20)
a2 ¶2f2/¶z2
+ (K R20) (a2) (¶Y2/¶z)2(1
– f2) –
- (k R20
) (f1 + f2) + (2k R20)
(1 – cosY2) -
- (k R20
) (1 – f2 )[1-cos(Y1 + Y2)]
; (5)
(m R20)
(1 – f1) 2 (d2Y1/dt2) – 2 (m R20)
(1 – f1) (df1/dt) (dY1/dt)
=
+ (KR20)
(a)2 (¶2Y1/¶z2)
(1- f1)2 – 2(K R20) (a2)
(¶Y1/¶z)
[¶f1/¶z ] (1- f1 ) –
- (2kR02)
(1- f1) [(sinY1)] +(k R20
) (1 – f2)( 1 – f1)[sin(Y1 + Y2)]
; (6)
(m R20)
(1 – f2) 2 (d2Y2/dt2) – (2m R20)
(1 – f2) (df2/dt) (dY2/dt)
=
+ (K R20)
(a)2 (¶2Y2/¶z2)
(1- f2)2 – 2(K R20) (a2)
(¶Y2/¶z)
[¶f2/¶z] (1- f2 )-
- (2kR02)
(1- f2) [(sinY2 )] + (k R20
) (1 – f2)( 1 – f1)[sin(Y1 + Y2)]
; (7)
где vi = R0 fi (i =
1,2.). Соответствующий уравнениям (5)–(8) модельный гамильтониан имеет вид
H = (rm R20/2)
ò dz [(¶f1/¶t)2
+ (¶f2/¶t)2] +
+ (Y R20/2)
ò dz [(¶f1/¶z)2
+ (¶f2/¶z)2] +
+ (y R20
/2 ) ò dz (f1 +
f2)2 +
+ (rm
R20/2) ò dz [(1- f1 )2
(¶Y1/¶t)2
+ (1- f2 )2(¶Y2/¶t)2]
+
+ (Y R20/2)
ò dz [(1- f1 )2
(¶Y1/¶z)2
+ (1- f2 )2 (¶Y2/¶z)2]
+
+ (y R02)
ò dz {2 (1-f1) (1-
cosY1) + 2 (1-f2) (1-
cosY2 ) +
+ (-f1 f2
+ f1 + f2-1 ) [1 – cos(Y1
+Y2)]}; (9)
Проблема, которую остается
решить – это поиск решений этих уравнений. Эта задача может быть решена в
адиабатическом приближении. Действительно, наша модельная система состоит из
двух подсистем. Первая описывает вращательные движения (переменные Y1
и Y2), вторая – поперечные
движения (переменные f1 и f2). Если предположить, что
вращательные движения являются значительно более медленными движениями по
сравнению с поперечными движениями, можно провести усреднение по поперечным
движениям и получить модельный гамильтониан для первой подсистемы в виде
Htors. = E0
+ [rm <(1- f1 )2>
R20/2] ò dz (¶Y1/¶t)2
+ [rm <(1- f2 )2>
R20/2] ò dz (¶Y2/¶t)2
+
+ [Y <(1- f1
)2> R20/2] ò dz (¶Y1/¶z)2
+ [Y<(1- f2 )2> R20/2]
ò dz (¶Y2/¶z)2
+
+ [ y <(1-f1)>
R02] ò dz [2 (1- cosY1)]
+ [rk <(1-f2)> R02]
ò dz [2 (1- cosY2
)] +
+ [y <(-f1 f2
+ f1 + f2-1 )> R02] ò dz [1 – cos(Y1 + Y2)]; (10)
где E0 – среднее значение энергии
вращательных колебаний, а < ... > означает усреднение по состояниям этой
подсистемы.
Модельный гамильтониан второй
подсистемы может быть получен, если мы предположим, что переменные Y1
и Y2 в уравнении (9) константы.
Hosc. = (rm
R20/2) ò dz [(¶f1/¶t)2
+ (¶f2/¶t)2] +
+ (Y R20/2)
ò dz [(¶f1/¶z)2
+ (¶f2/¶z)2] +
+ (y R20
/2 ) ò dz (f1 +
f2)2 +
+ (y R02)
ò dz {2 (1-f1) (1-
cosC1) + 2 (1-f2) (1- cosC2 ) +
+ (-f1 f2
+ f1 + f2-1 ) [1 – cos(C1 + C2)]}; (11)
Если предположить граничные
условия для торсионной подсистемы в виде
cosY1 ®
1, when Y1 ®
±¥; (12)
cosY2 ®
1, when Y2 ®
±¥; (13)
и учесть, что тогда
C1 = C2 =
0.
(14)
(1- cosC1 ) = (1- cosC2 ) = [1 – cos(C1 + C2)]
= 1- cos 0 cos0 + sin0 sin0 = 0; (15)
окончательный вид гамильтониана первой подсистемы
приобретет вид
Hosc. = (rm
R20/2) ò dz [(¶f1/¶t)2
+ (¶f2/¶t)2] +
+ (Y R20/2)
ò dz [(¶f1/¶z)2
+ (¶f2/¶z)2] +
+ (y R20
/2 ) ò dz (f1 +
f2)2 . (16)
Таким образом, в
адиабатическом приближении торсионная подсистема не оказывает влияния на
поперечные колебательные движения, а влияние поперечных колебаний на торсионную
подсистему приводит к простой перенормировке коэффициентов гамильтониана (и
уравнений) торсионной подсистемы. Такая перенормировка, в свою очередь влияет
на решения уравнений и приводит к увеличению размера, энергии, и массы
солитонов (кинков и антикинков).
Литература.
1.
J.D.
Watson and F.N.C. Crick, Nature 171 (1953) 737.
2.
F.H.C.
Crick and J.D. Watson, Proc. Roy. Soc. (London) A-223 (1954) 80.
3.
J.A.
McCommon and S.C. Harvey, Dynamics of Proteins and Nucleic Acids (Cambridge
University Press, Cambridge, 1987).
4.
L.V.
Yakushevich, Nonlinear Physics of DNA (John Wiley & Sons, Chichester,
1998).
5.
S.W.
Englander, N.R. Kallenbach, A.J. Heeger, J.A. Krumhansl and A. Litwin, Proc.
Natl. Acad. Sci. USA 77 (1980) 7222.
6.
S.
Yomosa, Phys. Rev. A-27 (1983) 2120.
7.
S.
Takeno and S. Homma, Prog. Theor. Phys. 70 (1983) 308.
8.
J.A.
Krumhansl and D.M. Alexander, in: Structure and Dynamics: Nucleic Acids and
Proteins, eds. E. Clementi and R.H. Sarma (Adenine Press, New York, 1983) pp.
61-80.
9.
V.K.
Fedyanin and V. Lisy, Stud. biophys. 116 (1986) 65.
10.
Ch.-T.
Zhang, Phys. Rev. A-35 (1987) 886.
11.
Yakushevich
L.V. Phys. Lett. A-136 (1989) 413.
12.
V.K.
Fedyanin and L.V. Yakushevich, Stud. biophys. 103 (1984) 171.
13.
K.F.
Baverstock and R.D. Cundal, Int. J. Radiat. Biol. 55 (1989) 152.
14.
L.V.
Yakushevich, Stud. biophys. 121 (1987) 201.
15.
R.V.
Polozov and L.V. Yakushevich, J. Theor. Biol. 130 (1988) 423.
16.
M.
Salerno, Phys. Lett. A-167, (1992) 49.
17.
M.
Peyrard and A.R. Bishop, Phys. Rev. Lett. 62 (1989) 2755.
18.
T.
Dauxois, M. Peyrard and C.R. Willis, Phys. D-57 (1992) 267.