1. Введение.
Начиная с работ А. Лотка [1],
В. Вольтерра [2] модели типа «хищник–жертва» применяются для анализа качественных
особенностей динамики взаимодействующих популяций. Модель «хищник-жертва» в
классической форме имеет вид:
Nt = f(N) N – B(N,P)P
Pt = kB(N, P)P – q(P)P,
где N, P – численности жертвы и хищника, f(N), q(P) – соответственно коэффициенты
размножения (гибели) жертвы (хищника) в «отсутствии друг друга», B(N,P)- трофическая функция хищника,
положительный коэффициент k <1.
В модели Вольтерра f(N) = r, g(P) = q, B(N, P) = sN при
положительных постоянных r, q, s.
Известно, что фазовыми траекториями такой модели в квадранте
(N >0, P>0) являются стационарная точка и предельные циклы, окружающие ее. Таким
образом, в системе Вольтерра существуют эндогенные колебания численности
популяций (впрочем, структурно неустойчивые в силу «переупрощенности» предположений
модели).
Учет конкуренции в популяции
жертвы, возникающей при большой численности, привел к модификации функции
размножения f(N). В частности, для
модели «хищник–жертва» с логистической функцией роста f(N)N=rN(1-N) показана
возможность устойчивого стационарного сосуществования популяций (см., например,
[3, 6]).
Принципиальная модификация
модели Вольтерра связана с учетом явления насыщения в популяции хищника при
росте численности популяции жертвы. Трофическая функция хищника, в простейшем
случае, принимает вид B(N)=sN/(1+sN),
s=сonst>0 ([3, 4, 5] и др.).
Модели с трофическими
функциями такого типа при различных функциях размножения жертвы и гибели
хищника и вариации параметров исследовались многими авторами. В их рамках была
показана возможность существования структурно устойчивых автоколебаний, описаны
многие эффекты, наблюдаемые в системах «хищник-жертва». Особо выделим работы
А.Д. Базыкина [6], применившего подходы теории бифуркаций при составлении и
исследовании таких моделей и указавшего ряд критериев приближения к границам
смены режимов.
Новая модификация
классической модели «хищник-жертва» была предложена в работе [7] (и
последующих), где дано экологически обоснованное предположение о том, что
трофическая функция хищника должна быть функцией не одной переменной N и не двух независимых переменных N и P,
а одной переменной – отношения численностей z=N/P,
то есть B(N,P)=g(z). Модели, в
которых используются такие трофические функции, названы ratio-dependent models, или короче RD-моделями. В ряде работ
по моделированию сообществ (например,[8]) было показано, что RD-модели дают существенно лучший
прогноз, чем классические модели «хищник-жертва».
В RD-моделях простейшая (и наиболее часто используемая) трофическая
функция с насыщением принимает вид
B(N,P) =g(z) = sz/(1+sz) = sN/(P+sN),
при (N,P) Î (0,¥)2 \ (0,0),
B(N>0, 0) = 1, B(0,
P >0) = 0.
Данная работа посвящена
анализу RD-модели с логистической
функцией размножения жертвы ([8, 9] и др.):
Nt = rN(1-N) – sNP/(P+sN) (1)
Pt = sNP/(P+sN)
– qP,
где s, r, q – положительные
параметры.
«Масштабированием» переменных
N = sx, P = s2y, t=t(x+y)/r, (2)
и введением новых параметров:
n= s/r, m = 1/r, g = q/r (3)
система (1) приводится к виду
xt = x (1 – x )(x+y) – nxy
(4)
yt = -gy(x+y)
+ m xy
Системы (4) и (1)
эквивалентны в первом квадранте при (x,
y)¹(0,0). В модели (4)
трофические отношения «характеризуются» параметрами m и n, а скорость смертности хищников – параметром g.
В данной работе приводятся
результаты исследования модели (4) в зависимости от параметров (g,n,m) при неотрицательных (x,y).
2. Бифуркационный портрет системы.
У
системы (4) при всех значениях параметров в первом квадранте имеются
стационарные точки O(x=0,y=0) и A(x=1,y=0).
Точка O – сложная (негиперболическая),
структура ее окрестности при {x³0, y³0}
существенно меняется при изменении параметров. Оказалось, что при положительных
g,m,n
траектории системы, расположенные в («положительной») окрестности точки O,
образуют одну из следующих 4 структур: один гиперболический сектор; один
гиперболический и один «устойчивый» параболический секторы; один
гиперболический и один «неустойчивый» параболический секторы; эллиптический
сектор, соседствующий с двумя параболическими секторами.
Точка A – седло
для m>g и узел для m<g.
При m>g , n <m/(m – g) в системе имеется стационарная точка B(x*= 1-n (m – g)/m, y*= (m – g)(m – n (m – g))/(mg)) –
топологический узел (фокус). Она появляется в первом квадранте для m = g через транскритическую бифуркацию с точкой A, и
исчезает, сливаясь с точкой O,
для n = m/(m – g). При
вариации параметров точка B меняет устойчивость в бифуркации
Андронова-Хопфа с рождением устойчивого предельного цикла. Этот цикл
разрушается на гетероклиническом контуре, образованном сепаратрисами точек O и A.
Все
перечисленные бифуркации определяют структуру фазово-параметрического портрета
модели, который описывает следующая теорема.
Теорема 1. Пространство параметров (g,m,n) разбивается на 8 областей топологически различных фазовых портретов
системы (4), рассматриваемой в конечной части
квадранта {x³0, y³0} (рис. 1a, 1b).
Граничные поверхности между областями соответствуют следующим бифуркациям:
BO: n = m/(m – g), BA: m = g – появление/исчезновение нетривиальной особой точки B;
M: m = g +1, n < g +1, N: n = g +1, m < g +1 –
смена топологической структуры особой точки O в первом квадранте, при
которой появляется/исчезает параболический сектор, содержащий траектории,
стремящиеся к точке O при t ®¥ (граница M), или стремящиеся к точке O при t ®-¥ (граница N);
H: n = m(g + m/(m -g))/(m+ g), g <m< g +1 – бифуркация Андронова-Хопфа, происходящая
с точкой B, пересечение границы H сопровождается
рождением/исчезновением устойчивого предельного цикла;
L – гетероклиническая бифуркация, при которой устойчивый предельный цикл
появляется/исчезает на контуре, образованном точками A и O и их общими
сепаратрисами[2].
Если m _ g +1, n _ g +1, то каждая характеристическая траектория
особой точки O обладает
асимптотикой, принадлежащей к одному из следующих трех типов
Тип 1:
y = Cxg /(n -1)(1+ o(1)) (C -произвольная постоянная),
который соответствует траекториям, стремящиеся к
точке O при t ® _. Траектории с такими асимптотиками существуют для
n > g +1;
Тип 2: y = Cxm – g (1+ o(1)) (C -произвольная постоянная),
который соответствует траекториям, стремящиеся к
точке O при t ® -_.. Траектории с такими асимптотиками
существуют для m > g + 1;
Тип 3: y = K x (1+ o(1)), где K = (m – g – 1)/( g+ 1-n)>0,
В этом виде представляется сепаратриса точки O при g+1<n<m/(m-g), а также семейство характеристических траекторий
в параметрических областях
{n>m/(m-g),
g <m<g+1} и {m/(m-g)<n<g+1, m >g+1}.
При значениях параметров o: n = g +1 = m система (4) имеет первый интеграл:
(g +1)ln((x+y)/x) – y (1+g/x) = C , где C –
произвольная постоянная.
Параметрический портрет
модели (4), отвечающий неотрицательным значениям фазовых переменных,
схематически представлен на плоскости параметров (m,n) для «типичного» значения параметра g (рис.
1a). Все указанные граничные
поверхности отвечают бифуркациям коразмерности 1 и на портрете являются граничными
кривыми; общие точки этих кривых отвечают бифуркациям коразмерности ³2.
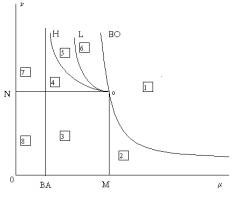
Рис. 1а. Параметрический
портрет системы (4) на плоскости параметров (m,n).
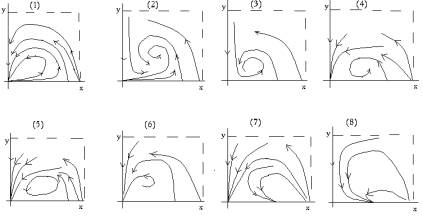
Рис. 1б. Фазовые портреты
системы (4) в соответствующих областях ее параметрического портрета на рис. 1а
Доказательство теоремы
проведено аналитическими и численными методами теории бифуркаций (см.,
например, [10]). При исследовании сложной особой точки O применялся специальный
метод, ассоциированный с диаграммой Ньютона [11].
3. Интерпретация бифуркационного портрета.
Каждая из 8 областей, на
которые разбивается параметрическое пространство модели, отражает особенности
динамических режимов сосуществования и/или вымирания популяций, входящих в
систему «хищник-жертва». Некоторые из параметрических областей могут быть
объединены, так как режимы, соответствующие им, отличаются несущественно с
точки зрения интерпретации. «Обобщенный» параметрический портрет (рис. 2)
содержит лишь 5 областей, среди которых:
·
область I, объединяющая области 1 и 6 параметрического
портрета из рис. 1а, соответствует вымиранию обеих популяций независимо от
начальных численностей хищника и жертвы;
·
область II, объединяющая области 2 и 3, соответствует
сосуществованию обеих популяций при любых начальных численностях хищника и
жертвы;
·
область III объединяет области 4 и 5. Здесь обе популяции
(жертвы и хищники) либо сосуществуют, либо вымирают, причем динамический режим,
который реализуется в системе, определяется значением отношения начальных численностей популяций. Заметим, что
сосуществование может быть стационарным (область 4) или колебательным (область
5);
Подчеркнем,
что поведение системы в области III существенно отличает рассматриваемую
RD-модель от других моделей «хищник-жертва».
·
область IV совпадает с областью 7, а область V – с
областью 8. В обеих этих областях популяция хищника вымирает при любых ее
начальных значениях. Заметим, что области V отвечает стационарный режим
существования популяции жертв, который «достигается» при любых начальных
численностях, тогда как в области IV, в зависимости от начальных значений, эта
популяция либо вымирает, либо переходит в стационарный режим существования
(аналогично динамическим режимам системы в областях II и III).
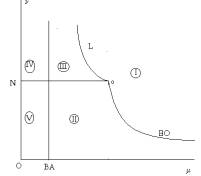
Рис. 2.
Интерпретационный параметрический портрет системы (4) на плоскости параметров (m,n).
Области
I и II имеют общую границу (нижняя часть кривой BO на рис. 2; области I и III имеют общую границу L. Пересечение этих границ из областей II и III в область I «влечет» вымирание
обеих популяций жертв и хищников.
Области
II и V, так же как области III и IV, имеют общую границу BA. Пересечение этой границы «влечет» вымирание лишь популяции
хищника.
Заметим,
что область I не имеет общих границ с областями IV и V. Это означает, что
переход из областей «гибели хищника» (IV, V) в область «гибели всей системы»
(I) возможен лишь через «область сосуществования» (области III или II).
Границы
областей II и III (кривые BA, L и «нижняя» часть BO на рис. 2, а также
граница N между областями II и III – «опасные»,
так как система может перейти к режиму вымирания при их пересечении. Этот
переход сопровождается:
·
ростом
периода автоколебаний – вблизи границы L,
·
уменьшением
равновесной (стационарной) численности жертвы – вблизи границы BO, и
уменьшением равновесной (стационарной) численности хищника – вблизи границы BA,
·
замедлением
восстановления популяции жертв при существенном уменьшении хищников – вблизи
границы N , разделяющей области II и III.
Наблюдение таких явлений в
системе может рассматриваться как знак приближения к опасной границе.
Литература.
1.
Lotka
A.J. Elements of physical biology. Baltimore: Williams and Wilkins, 1925.
2.
Вольтерра
В. Математическая теория борьбы за
существование. 1931 / Пер. с французского под ред. Ю.М.Свирежева. – М.: Наука,
1976.
3.
Maynard
Smith J. Models in ecology. Camdridge
University Press, London.NY, 1974.
4.
Holling
C.S. The functional response of
predator to prey density and its role in mimicry and population regulation. –
Mem. Entomol. Soc. Canada. – 1965. –V.45. –P.1-60.
5.
Алексеев
В.В. Влияние фактора насыщения на динамику системы хищник-жертва // Биофизика. – 1973. – Т.18.
– Вып.5. – С.922-926.
6.
Базыкин
А.Д. Математическая биофизика
взаимодействующих популяций. – М.: Наука, 1985.
7.
Arditi
R., Ginzburg L.R. Coupling in predator-prey dynamics: ratio-dependence, J.
Theor. Biol. – 1989. – 139. – P.311-326.
8.
Aksakaya
H.R., Arditi R., Ginzburg L.R. Ratio-dependent predation: an abstraction that
works, Ecology. – 1995. – 76. –
P.995-1004.
9.
Jost
C., Arino O., Arditi R. About deterministic extinction in ratio-dependent
predator-prey models. Bull. Math. Biol. – 1999. – 61. –
P.19-32.
10.
Kuznetsov
Yu. Elements of Applied Bifurcation Theory. Springer. – 1995.
11.
Березовская Ф.С.
Алгоритм исследования сложных стационарных точек двумерных моделей // Математическое
моделирование биологических процессов. – М. Наука, 1979. – C.105-116.