ВОЗМОЖНАЯ РОЛЬ РЕЗОНАНСА ФЕРМИ В ДИНАМИКЕ ФЕРМЕНТОВ

 

Карговский А.В., Кроо С.В., Ходжер О.П.

 

(Москва)

 

В работе аналитическими и численными методами исследуется резонанс Ферми в системе, моделирующей колебания субстрата или продукта реакции в активном центре фермента. Определяется частота перекачки энергии между модами колебаний. Обсуждается возможное влияние резонанса Ферми на скорость ферментативного акта.

 

THE POSSIBLE ROLE OF THE FERMI RESONANCE IN THE DYNAMICS OF ENZYMATIC MOLECULES

 

Kargovsky A.V., Kroo S.V., Khojer O.P.

 

(Moscow)

 

In this paper by analytical and numerical methods the Fermi resonance in the system that simulate fluctuations of substrate or a product of reaction in the active site of enzyme is investigated. The frequency of energy exchange between the oscillation modes is calculated. The possible influence of the Fermi resonance on the rate of enzymatic reaction is considered.

 

Исследованию молекул ферментов как сложных нелинейных систем посвящено множество работ в области молекулярной динамики [1-4]. Мы рассмотрели возможное значение модуляционных режимов обмена энергией между модами колебаний молекул при ферментативном катализе. Впервые модуляционные режимы обмена энергией между модами колебаний молекул обнаружил Э.Ферми [5], анализируя рамановские спектры газообразного CO2 методом возмущений. В молекуле CO2 частота продольной моды (1330 см-1) практически совпадает с удвоенной частотой поперечной моды (667,5 см-1), что приводит к появлению дополнительных полос в рамановских спектрах. Маятник с двумя колебательными степе­нями свободы — простейший классический аналог такой системы. Резонанс Ферми также возможен в протеиновых структурах потому, что частота продольных колебаний N-H близка к удвоенной частоте амида II, на что впервые указал М.В. Волькенштейн в 1947 году [6].

В данной работе изучается поведение молекул продуктов катализа, удерживаемых в активном центре (АЦ) фермента посредством нескольких водородных связей. Мы рассмотрели двумерную модель, в которой масса притягивается к стенкам четырьмя пружинами. Мы полагаем, что такая модель позволяет определить главные характеристики движения субстрата (или продукта реакции) внутри АЦ фермента. Параметры модели соответствуют активному центру фермента альфахимотрипсина. Жесткости пружин зависят от числа и направлений водородных связей, которые удерживают субстрат в АЦ. Даже в случае линейных пружин динамика системы существенно нелинейна, что делает возможным резонанс Ферми.

Реальная же система находится под действием молекул воды, а движения кластеров носят характер цветного шума.

Альфахимотрипсин: возможный объект с резонансом Ферми

Молекула фермента альфахимотрипсина состоит из двух субглобул A и B, соединенных «шарниром» (рис. 1). Активный центр фермента находится между субглобулами; важный элемент АЦ – комплекс с водородной связью N…HO (рис. 2). Субстрат, как показано в правой части рис. 1, удерживается в активном центре водородными связями и может колебаться с малой амплитудой.

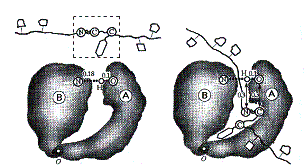
Рис. 1. Фермент a-химотрипсин.

 

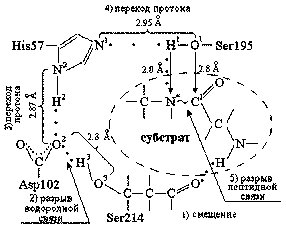
Рис. 2. Детальная схема активного центра a-химотрипсина.

 

 

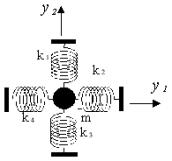
Рис. 3. Схема двумерной кластерной модели; m-масса кластера;

ki (i=1..4)-коэффициенты при квадратичных членах потенциала,

моделирующего водородные связи.

 

Базовая двумерная кластерная модель

Рассмотрим субстрат, удерживаемый в активном центре водородными связями, как массу, связанную четырьмя линейными пружинами с неподвижными стенками, которые соответствуют массивным белковым кластерам (рис. 3).

Динамика системы в координатах y1, y2 описывается уравнениями:

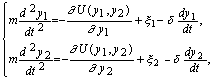                                                                     (1)

где xi– шум по соответствующей координате, d– декремент затухания системы.

Сначала рассмотрим систему (1) без затухания и шумов. Потенциальная функция системы в случае линейных пружин записывается следующим образом:

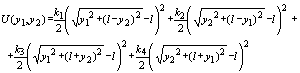                                                               (2)

Здесь 2 — расстояние между стенками.

Заметим, что, несмотря на линейный характер действующих на систему сил, динамика системы нелинейна.

Для случая малых колебаний y1, y2 << l (e << 0.1, где e = a/l, a — максимальная амплитуда колебаний, l-длина водородной связи) система уравнений может быть линеаризована. В результате наблюдаются две независимые моды колебаний с собственными частотами , . Резонанс Ферми реализуется при .

Подставляя (2) в (1) и раскладывая в ряд Тейлора вблизи точки равновесия до членов второго порядка, имеем:

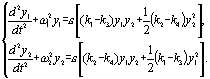                                                                      (3)

Данная система получена в предположении, что длина водородной связи l = 1 и масса кластера m = 1.

Аналитическое исследование

Теперь мы используем приближенные асимптотические методы Боголюбова и Митропольского и покажем, что энергия колебаний в консервативной системе (3) периодически перекачивается из моды “y1” в моду “у2” с некоторой частотой W [2].

С помощью метода медленно меняющихся амплитуд и фаз [7], будем искать уi (i=1, 2) в виде

Здесь Ai(t) и ji(t) — медленные по сравнению с периодами Тi=2p/wi функции времени. Тогда получим:

,

,

,

,

где Линия сверху означает процедуру усреднения по времени. Усредняя по периоду T 1 =2p /w1 (в случае w2 = 2w1) имеем:

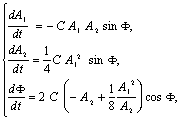                                                                                 (4)

где    C=,    F=2f 1 – f 2.                                                                                         (5)

Получим следующий интеграл системы (4):

.                                                                                                              (6)

Чтобы установить связь фазы F и амплитуд А1 и А2, воспользуемся последним уравнением системы (4), умножив его на :

                                                                           (7)

Так как  то  Исключая А1 с помощью (4.8), получим

или

В итоге имеем:

                                                                                                                 (8)

D — константа интегрирования.

Стационарные значения получаются из равенств:

Используя интегралы системы, получим

Таким образом, стационарные решения зависят от А0, то есть от начальных условий.

Резонансный обмен энергией в случае малых отклонений от положения равновесия характеризуется частотой модуляции W:

,                                                                                                  (9)

которую можно получить, линеаризируя систему (4).

Найдем период перекачки энергии в общем случае. Для этого выразим из (8) sinФ и подставим его в первое уравнение системы (4)

отсюда период перекачки энергии равен:

,                     (10)

где .

 найдем из условия :

                                                                                  (11)

Рассмотрим уравнение . Видно, что два его старших корня z2,3 совпадают с  и  при :

, , где.

Поскольку при z1<z2<z3

,

 где K(k) — полный эллиптический интеграл первого рода,

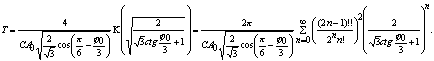
При выводе соотношения использован тот факт, что .

На рис. 4 мы представили численное решение системы (4). Предполагалось, что масса кластера m=100 а.е.м., k1=k, k2=0,5k, k3=2k, k4=0,25k, где k=51 Н/м – «жесткость» одной водородной связи.

Период перекачки энергии, расчитанный из численных решений при различных параметрах, хорошо соответствовал полученному аналитическому выражению (наблюдалось совпадение значений в пределах ошибки численной схемы).

Частоты набивки не показаны. Временной масштаб: 1 ед. = 0.1 пс; амплитудный масштаб: 1 ед. =2.

 

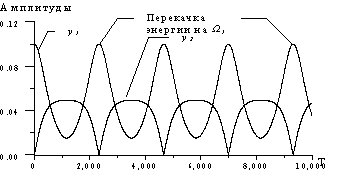
Рис. 4. Положительные огибающие амплитуд y1 и y2 в консерватив­ной системе.

 

Мы исследовали консервативную систему. Теперь рассмотрим систему с затуханием, в которой роль шума играет внешняя периодическая сила. Учитывая это, можно записать уравнения, аналогичные (3), в случае, когда в направлении 1 действует внешняя периодическая сила и сила трения:

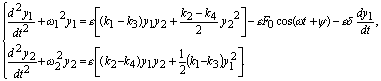           (12)

Здесь F0 — амплитуда внешней периодической силы частоты w, а d — декремент затухания системы.

Так как мы рассматриваем лишь члены порядка e, на d и F0 накладываются следующие приближенные равенства:

,

где и  — максимальные амплитуды огибающих y1(t) и y2(t).

Будем искать решение (12) в первом приближении при w=w1 в виде

В случае резонанса w1=w=w2/2 можно произвести процедуру усреднения уравнений (12):

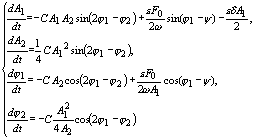                                                      (13)

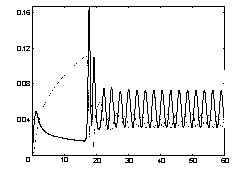
Попытка аналитического исследования полученной системы к настоящему времени не принесла результатов. Численное решение системы (13) представлено на рис. 5.

Амплитуды

 

 

Рис. 5. Положительные огибающие амплитуд y1 (сплошная линия) и y2 (пунктирная линия) в диссипативной системе с внешней силой.

Масштаб, масса кластера и жесткости пружин такие же, как на рис. 4. F0=0,05, δ=0,5.

Нами также рассматривался случай, когда периодические внешние силы действуют по обеим координатам с частотами, совпадающими с собственными в соответствующих направлениях.

У2
 

У1
 

 

 

 

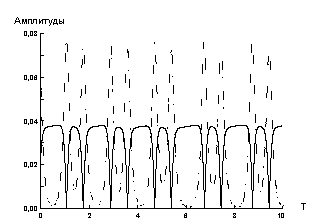
Рис. 6. Положительные огибающие амплитуд y1  и y2 в диссипативной системе с двумя внешними силами.

Масштаб, масса класте­ра и жесткости пружин такие же, как на рис. 4.

Численный эксперимент демонстрирует, что модуляционный режим обмена энергией реализуется и в такой системе (рис. 6).

Заключение

Используя метод медленно меняющихся амплитуд, мы аналитически описали поведение автономной системы в модуляционных режимах и получили выражение для скорости передачи энергии. Численный эксперимент доказал существование модуляционных режимов в модели, учитывающей периодическую внешнюю силу и вязкое трение.

Помимо изложенных случаев автономной системы и системы с периодическими внешними силами нами также исследовалось движение пробной частицы под воздействием белого шума. Численное решение показывает наличие модуляционных режимов и в этом случае.

Таким образом, нами рассмотрены две «крайних» ситуации: периодическое и чисто случайное воздействия. В реальной системе внешнее воздействие носит характер цветного шума, и, следовательно, мы можем ожидать наличие модуляционных режимов колебания субстрата или продуктов реакции вблизи активного центра фермента.

Исследованные режимы колебаний могут оказывать существенное влияние на процесс ферментативного катализа. Высокая концентрация энергии в выделенной степени свободы вследствие резонанса Ферми увеличивает вероятность выхода продуктов реакции из активного центра и таким образом увеличивает скорость ферментативного акта.

Необходимо отметить, что точное выполнение условий резонанса Ферми w1=2w2 может встречаться только в ограниченном числе конформаций белка, реализующихся при медленных структурных изменениях молекулы.

Работа поддержана грантом РФФИ 01-03-33163.

Авторы выражают благодарность профессору Романовскому Юрию Михайловичу за постановку задачи и полезные обсуждения.

 

Список литературы:

1. A.V. Netrebko, N. V. Netrebko, Yu. M. Romanovsky, Yu. I. Khurgin, W. Ebeling. Stohastic cluster dynamics of enzyme-substrate complex. Applied Nonlinear Dynamics 3 (1996) 53.

2. E.Shidlovskaya, L. Schimansky-Geier, Yu. M. Romanovsky. Nonlinear vibra­tions in 2-dimensional protein cluster model with linear bonds. Z Phys. Chem. Leipzig 214, 1 (2000) 65.

3. Yu. M. Romanovsky, A.V. Netrebko. Some problems of cluster dynamics: models of molecular scissors. Applied Nonlinear Dynamics 4 (1998) 31.

4. Молекулярная динамика ферментов. Под редакцией Ю. М. Романовского и В. Эбелинга. Изд. МГУ, Москва (2000).

5. E. Fermi. Über den Ramaneffect des Kohlendioxyds. Zs. F. Phys. 71 (1931) 250.

6. М. В. Волькенштейн. Строение молекул. М., Л.:Изд-во АН СССР, 1947.

7. Н. Н. Боголюбов, Ю. М. Митропольский. Ассимтотические методы в теории нелинейных колебаний. Наука, Москва (1974).