ФИЗИЧЕСКИЕ ПОДХОДЫ В ИССЛЕДОВАНИЯХ ДНК

Якушевич Л.В.

(Пущино)

В данной работе обсуждается взаимодействие физики и науки о ДНК. Мы показываем, что такое взаимодействие приводит к появлению новых интересных физических моделей с оригинальными гамильтонианами, динамическими уравнениями и решениями.

PHYSICAL MODELS IN DNA SCIENCE

Yakushevich L.V.

(Pushchino)

It is widely accepted now that physical ideas and methods deeply penetrate to biology. This process is useful for both physics and biology. But in recent report made at the Workshop "Biological Physics 2000", Hans Frauenfelder has noted that although physics and biology have interacted at least since Galvani, the connection between them looks like a two-way street with the heavy traffic has gone one way (many tools from physics have been adopted by researchers in the biological sciences), and the return traffic, where biological ideas motivate physical considerations, has been less visible [1].

In this paper we just consider the "return traffic". As an example, we took the problem of interaction of nonlinear physics and mathematics with DNA science, and we discuss what new ideas, physical models, mathematical equations gave this interaction.

1. New dynamical models

The history of the penetration of the ideas of nonlinear physics and mathematics to DNA science began in 1980 when publication of the work of Englander and co-authors [2] gave a powerful impulse for physicists dealing with nonlinear systems to study DNA. This led to appearance of many interesting dynamical models. In this section we describe some of them.

From the first glance DNA is nothing but a system consisting of many atoms interacting with one another and organized in a special way in space. Under usual external conditions (temperature, pH, humidity, etc) this space organization has the form of the double helix which is rather stable but moveable system. The thermal bath where the DNA molecule is usually immersed is one of the reasons of the DNA internal mobility. Collisions with the molecules of the solution which surrounds DNA, local interactions with proteins, drugs or with some other ligands also lead to internal mobility. As a result, different structural elements of the DNA molecule such as individual atoms, groups of atoms (bases, sugar rings, phosphates), fragments of the double chain including several base pairs, are in constant movement. So, from the point of physics, the DNA molecule can be considered as a complex dynamical system with large number of internal motions.

How to model the system? Physicists proposed many dynamical models. The main models were gathered in [3, 4] and we present them here in the table 1. For convenience the models are arranged in the order of increasing their complexity and each new level of complexity is presented as a new line in the table.

Table 1. Approximate models of DNA structure and dynamics.

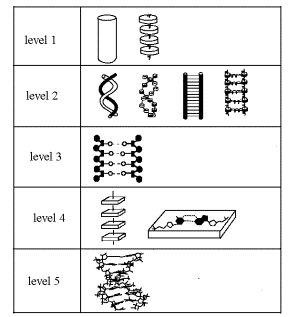
In the first line of the table, the simplest models of DNA, namely, the model of elastic thread and its discreet version, are shown. These models are too simple and they are not original.

In the second line of the table, more complex models of the internal DNA dynamics are shown. They take into account that the DNA molecule consists of two polynucleotide chains. The first of the models consists of two elastic threads weakly interacting with one another and being wound around each other to produce the double helix. The discreet version of the model is nearby. The next two models in the line are simplified versions of the previous two models, which are often used by investigators. In these models the helicity of the DNA structure is neglected. The model of this line looks rather original. They have not any analogy in physics.

In the third line a more complex model of the DNA internal dynamics is shown. It takes into account that each of the chains consists of three types of atomic groups (bases, sugar rings, phosphates). In the Table 1 different groups are shown schematically by different geometrical forms, and, for simplicity, the helicity of the structure is omitted.

The models of this line have not any analogy in physics too.

The list of models could be continued and new lines with more and more complex models of DNA structure and dynamics could be added till the most accurate model which takes into account all atoms, motions and interactions, would be reached. And there are not doubts that all of them are very original and have not analogy in physics.

2. New mathematical models

Let us illustrate now that interaction of DNA science with nonlinear mathematics does lead to new mathematical equations with new interesting solutions. For the purpose, we can refer to our previous work [5] where a new model hamiltonian and nonlinear dynamical equations describing internal DNA dynamics (in the framework of the models of second line of the table 1) have been obtained. Improved version of the hamiltonian, which has been recently obtained, is

H = (m/2) S_n {[(du_n,1/dt)² + (R₀ – u_n,1)² (dQ_n,1/dt)² + m(dz_n,1 /dt)²]

+ [(du_n,2/dt)² + (R₀ + u_n,2)² (dQ_n,2/dt)²+ m(dz_n,2 /dt)²]} +

+ (K/2) S_n {[ 2R²₀ [1- cos(Q_n,1 -Q_n-1,1 )] + u²_n,1+ u²_n-1,1 – 2 u_n,1 u_n-1,1 cos(Q_n,1 – Q_n-1,1 ) –

-2 R₀ u_n,1 [1 – cos(Q_n,1 -Q_n-1,1 )] – 2 R₀ u_n-1,1 [1 – cos(Q_n,1 -Q_n-1,1 )] + |z_n,1 – z_n-1,1 |² +

+ |z_n,2 – z_n-1,2 |²] + [2R²₀ [1- cos(Q_n,2 -Q_n-1,2 )] + u²_n,2+ u²_n-1,2 –

- 2 u_n,2 u_n-1,2 cos(Q_n,2 – Q_n-1,2 ) + 2 R₀ u_n,2 [1 – cos(Q_n,2 -Q_n-1,2 )] +

+ 2 R₀ u_n-1,2 [1 – cos(Q_n,2 -Q_n-1,2 )]]} + (k /2 )S_n {[ 2R₀²{(1 – 2 cosQ_n,1) +

+ (1 – 2cosQ_n,2 ) + [1 + cos(Q_n,1 -Q_n,2)] } – 2R₀ u_n,1 (1 – 2 cosQ_n,1)+

+ 2R₀ u_n,2 (1 – 2 cosQ_n,2) + u_n,1 ² + u²_n,2 – 2 u_n,1 u_n,2 cos(Q_n,1 – Q_n,2 ) –

- 2R₀ u_n,1 cos(Q_n,1 – Q_n,2 ) + 2R₀ u_n,2 cos(Q_n,1 -Q_n,2)] + k |z_n,1 – z_n,2 |² } ; (4)

where Q_n,i describes angular displacement of the n-th structural unit of the i-th chain; u_n,i describes the transverse displacement; z_n,i describes the longitudinal displacement (i = 1,2); m is a common mass of nucleotides; K is the coupling constant along each strand; R₀ is the radius of DNA; a is the distance between bases along the chains; and V is the potential function describing interaction between bases in pairs.

Hamiltonian (4) can be written in a more convenient form

H = H(f) + H(Y) + H(g) + H(interact.); (5)

where

H(f) = (m R²₀/2) S_n (df_n,1/dt)² + (m R²₀/2) S_n (df_n,2/dt)² + (K R²₀/2) S_n (f_n,1- f_n-1,1)² +

+ (K R²₀/2) S_n (f_n,2 – f_n-1,2)² + (k R²₀ /2 ) S_n (f_n,1 + f_n,2)²; (6)

H(Y) = (m R²₀/2) S_n (dY_n,1/dt)² + (m R²₀/2) S_n (dY_n,2/dt)² +

+ (KR²₀) S_n [1- cos(Y_n,1 – Y_n-1,1 )] + + (KR²₀) S_n [1- cos(Y_n,2 -Y_n-1,2 )] +

+ (kR₀²) S_n { 2 (1- cosY_n,1) + 2 (1- cosY_n,2 ) – [1 – cos(Y_n,1 +Y_n,2)]}; (7)

H(g) = (m R²₀/2) S_n (dg_n,1/dt)² + (m R²₀/2) S_n (dg_n,2/dt)² + (K R²₀/2) S_n (g_n,1- g_n-1,1)² +

+ (K R²₀/2) S_n (g_n,2 – g_n-1,2)² + (k R²₀ /2 ) S_n (g_n,1 + g_n,2)²; (8)

H(interact.) = (m R²₀/2) S_n (- 2 f_n,1 + f²_n,1) (dY_n,1/dt)² +

+ (m R²₀/2) S_n (-2f_n,2 + f _n,2²)(dY_n,2/dt)² +

+ (K R²₀) S_n [1-cos(Y_n,1 – Y_n-1,1 )] [f_n,1 f_n-1,1 – f_n-1,1 – f_n,1 ] +

+ (K R²₀) S_n [1-cos(Y_n,2 – Y_n-1,2 )] [f_n,2 f_n-1,2 – f_n,2 – f_n-1,2] -

- (2k R²₀) S_n (f_n,1) (1 – cosY_n,1) – (2k R²₀) S_n (f_n,2 ) (1 – cosY_n,2)+

+ (k R²₀) S_n (-f_n,1 f_n,2 + f_n,1 + f_n,2 ) [1-cos(Y_n,1 + Y_n,2)]; (9)

with new variables

f_n,1= u_n,1/R₀; f_n,2 = -u_n,2/R₀;

Y_n,1=Q_n,1; Y_n,2= -Q_n,2; (10)

g_n,1= z_n,1/R₀; g_n,2 = -z_n,2/R₀.

Here H(f) describes transverse motions; H(Y) describes torsional motions; H(g) describes longitudinal motions; H(interact.) describes interactions between the motions.

Usually it is suggested that the solutions are rather smooth functions (that is the functions f₁, f₂, g₁, g₂, Y₁, Y₁ change substantially only at the distances which are much more than the distance between neighboring base pairs), and continuos approximation is used. In the continuos approximation the model hamiltonian takes the form

H_cont. = (r_m R²₀/2) ò dz [(¶f₁/¶t)² + (¶f₂/¶t)²] + (Y R²₀/2) ò dz [(¶f₁/¶z)² + (¶f₂/¶z)²] +

+ (y R²₀ /2 ) ò dz (f₁ + f₂)² + (r_m R²₀/2) ò dz [(¶g₁/¶t)² + (¶g₂/¶t)²] +

+ (Y R²₀/2) ò dz [(¶g₁/¶z)² + (¶g₂/¶z)²] + (y R²₀ /2 ) ò dz (g₁ + g₂)² +

+ (r_m R²₀/2) ò dz [(1- f₁ )² (¶Y₁/¶t)² + (1- f₂ )²(¶Y₂/¶t)²] +

+ (Y R²₀/2) ò dz [(1- f₁ )² (¶Y₁/¶z)² + (1- f₂ )² (¶Y₂/¶z)²] +

+ (y R₀²) ò dz {2 (1-f₁) (1- cosY₁) + 2 (1-f₂) (1- cosY₂ ) +

+ (-f₁ f₂ + f₁ + f₂-1 ) [1 – cos(Y₁ +Y₂)]}; (11)

where m/a = r_m; Ka = Y; k/a = y. And the dynamical equations which correspond to the model hamiltonian (11), can be easily obtained from the general theory of hamiltonian systems

r_m (d² f₁/dt²) + r_m (1- f₁) (dY₁/dt)² = Y ¶²f₁/¶z² + Y (¶Y₁/¶z)²(1 – f₁) –

– y (f₁ + f₂) + 2y (1 – cosY₁) – y (1 – f₁)[1-cos(Y₁ + Y₂)] ; (12)

r_m (d² f₂/dt²) + r_m (1- f₂) (dY₂/dt)² = Y ¶²f₂/¶z² + Y (¶Y₂/¶z)²(1 – f₂) –

– y (f₁ + f₂) + 2y (1 – cosY₂) – y (1 – f₂ )[1-cos(Y₁ + Y₂)] ; (13)

r_m (1 – f₁) (d²Y₁/dt²) – 2r_m (df₁/dt) (dY₁/dt) = Y (¶²Y₁/¶z²) (1- f₁) –

– 2Y (¶Y₁/¶z) [¶f₁/¶z ] – 2y [(sinY₁)] + y(1 – f₁)[sin(Y₁ + Y₂)] ; (14)

r_m (1 – f₂) (d²Y₂/dt²) – 2r_m (df₂/dt) (dY₂/dt) = Y (¶²Y₂/¶z²) (1- f₂) –

– 2Y (¶Y2/¶z) [¶f2/¶z] – 2y [(sinY2 )] + y(1 – f1)[sin(Y1 + Y2)]. (15)

r_m (d² g₁/dt²) = Y ¶²g₁/¶z² – y (g₁ + g₂); (16)

r_m (d² g₂/dt²) = Y ¶²g₂/¶z² – y (g₁ + g₂). (17)

3. New models of inhomogeneity

Many different models of inhomogeneity are used in physics. The most popular of them are point inhomogeneity, boundary between two neighboring homogeneous ranges and random inhomogeneity. DNA gives us a new type of inhomogeneity, which is appeared due to the sequence of bases. Four types of bases (adenine, thymine, guanine and cytosine) forms the sequence which is specific and unique for any living organism.

In the models considered above, we ignored the difference between the bases. That is we considered the models like this

b b b b b b b b b b b

| | | | | | | | | | | (1)

b b b b b b b b b b b

where b denotes a base.

But model (1) is not correct even for homogeneous fragment of DNA (for example for synthetic polyA·polyT). Correct variant is

AAAAAAAAAAA

| | | | | | | | | | | (2)

TTTTTTTTTTTT

We could say that this fragment of DNA looks like a quasi-one dimensional crystal with two "atoms" (nucleotides) in the cell.

In real DNA, however, we have a sequence like this

AGCTTCGAAGG

| | | | | | | | | | | (3)

TCGAAGCTTCC

This type of inhomogeneity is very unusual from physical point of view.

6. Conclusions

In this paper we tried to show that interaction between nonlinear physics and DNA science looks rather promising not only for biology, but also for physics. We presented several examples to illustrate this statement. The list of examples could be continued by including many other interesting problems that appear due to the interaction. The problem of DNA-surrounding interaction, the problem of statistics of local distortions (unwound regions, for example) in DNA, the problem scattering of light and neutrons by DNA are only some of them. Moreover, we are sure that further investigations will bring us new examples confirming the statement.

References:

1. H. Frauenfelder Abstracts of The First Workshop on Biological Physics 2000 (September 18-22, 2000, Bangkok, Thailand) p. 13, 2000.

2. S.W. Englander, N,R. Kallenbach, A.J. Heeger, J.A. Krumhansl and A. Litwin, Proc. Natl. Acad. Sci. USA 77, 7222, 1980.

3. L.V. Yakushevich Quart. Rev. Biophys. 26, 201, 1993.

4. L.V. Yakushevich Nonlinear physics of DNA. Wiley, N.Y., 1998.

5. L.V. Yakushevich Mathematics. Computer. Education. 7, 696, 2000.