КВАНТОВОМЕХАНИЧЕСКИЕ И МАКРОДИНАМИЧЕСКИЕ АНАЛОГИИ В МАТЕМАТИЧЕСКОЙ ТЕОРИИ БИОЛОГИЧЕСКИХ СООБЩЕСТВ
(г. Пущино, Московская обл.)
Прослеживается связь между
вольтерровскими моделями математической экологии и дискретным нелинейным
уравнением Шредингера квантовой теории динамики возбуждений. Проведено
сведéние пространственно-распределённой модели растительного сообщества
к канонической форме уравнений макродинамики.
QUANTUM MECHANICAL
AND MACRODYNAMIC ANALOGIES IN MATHEMATICAL THEORY OF BIOLOGICAL COMMUNITIES
Yu.M. Aponin, E.A.
Aponina
(Pushchino, Moscow Region)
The relation between Volterra models
of mathematical ecology and discrete nonlinear Schrödinger equation is
considered. The spatially distributed model of plant communities is converted
to its macrodynamic analogy.
На протяжении всей истории развития математического естествознания различные формы аналогии служили источником новых идей и обобщений [1]. “Признание формальной аналогии между двумя системами идей, – писал Максвелл, – приводит к более глубокому познанию обеих, чем познание, которое можно было получить, изучая каждую систему в отдельности” ([2], стр. 8). Большую роль играет аналогия и в учебном процессе. Так, после изучения электростатики оказывается возможным получить точные сведения о многих явлениях, описываемых электростатическими аналогиями в ряде других областей физики ([3], гл. 12).
Однако более важными и интересными являются те случаи использования аналогии, когда она подсказывает пути обобщения математической модели с существенным расширением её области применимости. Например, глубокая аналогия между уравнениями механики и уравнениями теории электрических цепей послужила основанием для уравнений Лагранжа – Максвелла, описывающих динамику электромеханических систем [4], знаменитая оптико-механическая аналогия сыграла важную роль в развитии квантовой физики.
Роль аналогий в развитии науки высоко оценил И. Кеплер: “Я особенно люблю эти аналогии, моих вернейших учителей, участников тайн природы, … ибо они охватывают бесчисленные случаи в своих пределах … и ясно обнаруживают перед нашими глазами сущность вещей” (цит. по: [1], стр. 67).
В последние годы, в связи с быстрым расширением области применения нелинейных дифференциальных уравнений в физике и биологии, стали обнаруживаться новые аналогии, отражающие сходство в поведении живых систем (например, биологических сообществ) и аналогичных им систем “неодушевлённой” природы, в том числе и систем, относящихся к атомно-молекулярному квантовомеханическому уровню. В настоящей статье рассматриваются примеры аналогий такого рода. Прослеживается связь между дискретным нелинейным уравнением Шредингера (ДНШ), вольтерровскими моделями математической экологии и канонической формой уравнений макродинамики.
Некоторые частные случаи ДНШ появились в литературе ещё в семидесятые годы в работах А.С. Давыдова по математическому моделированию динамики транспорта возбуждений в молекулах белков. В этих работах (см., например, [5]) молекула белка рассматривается как цепочка активных элементов – сайтов, на которых могут локализоваться возбуждения. Каждый из этих сайтов может находиться в основном и возбуждённых состояниях. Роль таких сайтов в белках играют пептидные группы, входящие в состав полипептидной цепи белковой молекулы. Возбуждение мигрирует по сайт-цепочке, локализуясь то на одном, то на другом её сайте. При этом могут происходить и процессы делокализации, когда возбуждение на некоторое время как бы рассредоточивается, распределяясь по некоторому множеству сайтов. Эти процессы миграции, делокализации и обратной локализации возбуждения описываются выведенными А.С. Давыдовым нелинейными квантовомеханическими уравнениями, которые и представляют собой частный случай ДНШ, записанного для квазиодномерной решёточной структуры. В общем случае ДНШ можно записать в следующем виде:
![]() (1)
(1)
Здесь t –
время, ya
– комплексная амплитуда, характеризующая количество и фазу возбуждения,
локализованного на сайте a.
Система уравнений (1) описывает динамику возбуждений на n сайтах, которые в общем случае образуют нерегулярную решёточную структуру. Предполагается, что матрица межсайтовых переходов А = (Аab) является комплексной эрмитовой матрицей с нулевыми диагональными элементами (вещественный параметр e введён для удобства). Матрица В = (Вab) характеризует влияние возбуждения на свойства решётки. Элементы этой матрицы, а также параметры В1, …, Вn , могут принимать комплексные значения.
Сделаем замену переменных в системе (1), полагая
![]() (2)
(2)
где Na = | ya|2 интерпретируется как количество возбуждения (число квазичастиц) на сайте a, а qa – фаза этого возбуждения, qa Î R. Тогда нетрудно убедиться, что относительно новых переменных N1, …, Nn получается следующая система уравнений:
![]() (3)
(3)
где N = (N1, …, Nn) , q = (q1, …, qn) , ba = 2 Im Ba , bab = 2 Im Bab , причём функции f1, …, fn легко вычисляются в явном виде.
При малых e система (3) аналогична
вольтерровской модели динамики взаимодействующих популяций, образующих в
совокупности некоторое биологическое сообщество. При этом квадрат модуля
квантовомеханической амплитуды ya, то есть переменная Na, является анáлогом численности популяции
вида a.
Есть основания полагать, что отмеченная здесь связь между ДНШ и вольтерровской моделью должна играть важную роль как в квантовой теории динамики возбуждений, так и в теории биологических сообществ, поскольку данная аналогия открывает возможность обмена информацией между этими разными областями знания. Теория вольтерровских систем достаточно богата по своим понятиям и результатам. Поэтому весьма вероятно, что квантовомеханическая интерпретация некоторых уже известных и хорошо изученных свойств вольтерровских моделей позволит обнаружить ряд новых и необычных типов динамики возбуждений в нерегулярных решёточных структурах. Кроме того, оказывается возможной классификация решений ДНШ на основе изучения их пределов при e ® 0 , то есть так называемых порождающих решений*. Порождающими решениями могут служить, например, периодические решения вольтерровских систем.
Особый интерес представляет вопрос о квантовомеханической интерпретации бесконечных множеств предельных циклов и сопутствующих им более сложных динамических режимов с чертами квазислучайного поведения, которые существуют в окрестности сепаратрисных контуров вольтерровских систем [7, 8]. Заметим, кстати, что существование устойчивых предельных циклов свидетельствует о неконсервативности системы (1) (за исключением случая конечного числа условий, типа равенства, на параметры ba, bab). Известно, что идея построения неконсервативных моделей квантовомеханических систем высказывалась ещё в ранний период развития квантовой механики Дж. Д. Биркгофом и А.А. Андроновым [9].
Интересно также выяснить квантовомеханическую интерпретацию полученных в математической экологии многочисленных результатов об условиях устойчивости биологических сообществ, сформулированных в виде ограничений на матрицу межпопуляционных взаимодействий, в том числе и ограничений структурно-топологического характера.
Рассматриваемая аналогия
представляет интерес и для теории биологических сообществ, так как она
подсказывает возможные обобщения вольтерровских моделей с переходом в
комплексное пространство состояний Cn. При этом каждая из взаимодействующих популяций
сообщества характеризуется не только своей численностью Na , но и второй переменной типа вращающейся фазы qa, которая описывает собственный, внутренний ритм
биологической популяции. Идея использования комплексного пространства состояний
при математическом моделировании живых систем обсуждается в современной
литературе [10].
Рассмотрим теперь каноническую форму уравнений макродинамики (см. [11, 12]):
![]() (4)
(4)
где q = (q1
, …, qn)*
Î
Rn![]() , G
= G(q) – гладкая
вещественная функция, А – вещественная
(n ´ n)-матрица. Здесь градиент ¶ G / ¶ q рассматривается
как матрица-строка, звёздочкой обозначена операция транспонирования матриц.
, G
= G(q) – гладкая
вещественная функция, А – вещественная
(n ´ n)-матрица. Здесь градиент ¶ G / ¶ q рассматривается
как матрица-строка, звёздочкой обозначена операция транспонирования матриц.
Макродинамическая модель (4) охватывает широкий класс систем, изучаемых в механике, гидродинамике, термодинамике [12, 13]. Например, такую структуру имеют феноменологические уравнения термодинамики необратимых процессов, предложенные Онзагером ещё в тридцатые годы. При этом А – это, так называемая, матрица переноса, а G – термодинамический потенциал, соответствующий выбранным равновесным граничным условиям (для изолированных систем G = ‑ S, где S – энтропия).
Известно, что вольтерровские модели математической экологии также могут быть представлены в виде (4), см. [14]. Замечательно, что при таком сведéнии аналогом матрицы переноса является матрица межпопуляционных взаимодействий в биологическом сообществе. Соответствующие макродинамические аналогии оказываются полезными при исследовании устойчивости биологических сообществ. В этой связи представляет интерес следующий результат о поведении в целом траекторий макродинамической модели.
Т е о р е м а. Пусть матрица А = А(q) системы (4) положительно определена при всех q Î Rn, причём её элементы являются гладкими функциями от q. Пусть, кроме того, М – множество положений равновесия системы (4) и M ¹ Æ . Тогда истинны следующие утверждения:
1) множество М совпадает с множеством стационарных точек функции G, то есть М = { q Î Rn | ¶ G/¶ q (q) = 0 };
2) любая ограниченная положительная (отрицательная)
полутраектория системы (4)
при t® + ¥ (t ® – ¥) стремится
к М.
Первое утверждение тривиально в силу невырожденности матрицы А. Нетрудно убедиться также, что функция G не возрастает на траекториях системы (4). Поэтому второе утверждение является простым следствием так называемого принципа инвариантности (см., например, [15]). Подчеркнём, что симметричность матрицы А не требуется.
С л е д с т в и е. Пусть выполнены условия теоремы и, кроме того, множество положений равновесия М дискретно. Тогда для любой ограниченной положительной (отрицательной) полутраектории системы (4) существует положение равновесия, то есть точка в М, к которому эта полутраектория стремится при t® + ¥ (t ® – ¥).
Это очевидное следствие приведённой выше теоремы и известного утверждения о связности множества предельных точек полутраектории динамической системы [15].
Рассмотрим теперь обобщение уравнений макродинамики (4) на пространственно-распределённые системы. Это обобщение имеет следующий вид:
![]() (5)
(5)
где q = q(x, t) и
![]() (6)
(6)
Функционал S аналогичен механическому действию с лагранжевой плотностью ![]() Здесь матрицы-столбцы
Здесь матрицы-столбцы
![]() Î
Rn и для простоты рассматривается случай только
одной пространственной переменной x Î R.
Î
Rn и для простоты рассматривается случай только
одной пространственной переменной x Î R.
Подставляя в (5) известное выражение для вариационной производной d S /d q, см. [16], получим следующую систему уравнений в частных производных:
![]() (7)
(7)
В таком виде можно представить целый ряд моделей типа реакция – диффузия, а также некоторые “шредингеровские” системы математической экологии, которые аналогичны уравнениям квантовой механики [17].
Исследование любых систем вида
(7) обычно начинается с изучения однородных по пространству решений. Ясно, что
эта задача сводится к исследованию системы (4) при G(q) = L(q,
0). Следующей задачей является изучение стационарных решений системы (7). И
здесь вновь оказывается полезной аналогия (теперь чисто механическая): если x рассматривать формально как время, то L можно интерпретировать как функцию
Лагранжа механической системы с обобщёнными координатами q1, … , qn.
Таким образом, стационарные решения системы (7) можно найти из уравнений
Лагранжа для соответствующей механической системы.
Заметим, что рассмотренная выше механическая аналогия часто используется в синергетике в тех случаях, когда для исследуемой модели легко угадывается способ приведения её к (А, L)-системе вида (7), см. [18]. Однако и в более сложных случаях (А, L)-форма уравнений оказывается полезной, особенно, если удаётся подобрать положительно определённую матрицу А = А(q). В этом случае (при некоторых дополнительных условиях, формулировку которых мы опускаем ввиду краткости изложения) справедливо утверждение о глобальном поведении траекторий, аналогичное приведённой выше теореме. Задача исследования таких систем сводится в основном к изучению их стационарных решений на основе отмеченной выше механической аналогии. Далее мы проиллюстрируем этот подход на конкретном примере из математической экологии.
Рассмотрим
предложенную в работе [19] модель сообщества растений с двумя возрастными
классами, учитывающую процессы производства и рассеяния семян. Обезразмеренные
уравнения этой модели имеют следующий
вид:
![]() (8)
(8)
где u, u, w – плотности популяций “молодых”, “старых” растений
и семян, функция g(u) = (u – 1)2
+ s является характеристикой
зависящей от u смертности особей младшего возрастного класса и
скорости их перехода в старший класс, h
– коэффициент смертности “старых” растений. Параметры b и r
характеризуют процессы осаждения, порчи и прорастания семян, рассеяние которых
описывается диффузионным членом w xx.
Нетрудно убедиться, что система (8) приводится к (А, L)-системе (7), если положить q = (u, u, w)* , q¢ = (ux , ux , w x)* ,
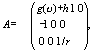 (9)
(9)
![]() (10)
(10)
где
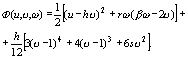 (11)
(11)
Заметим, что A
– невырожденная матрица. Поэтому на основании установленной ранее механической
аналогии изучение стационарных решений системы (8) сводится к исследованию механической
системы с функцией Лагранжа (10), если пространственную переменную
x
интерпретировать как время. Лагранжиан (10) соответствует системе
трёх материальных точек, движущихся по прямой, причем две из них имеют нулевую
массу, а масса третьей точки равна r.
Потенциальная энергия P этой
системы противоположна по знаку eё силовой функции: P = – F.
Такая
интерпретация немедленно приводит к содержательному следствию: механическая система
имеет первый интеграл ![]() – закон сохранения
энергии системы. Полученные результаты позволяют полностью исследовать на
основании установленной механической аналогии стационарные решения модели (8).
Мы не останавливаемся подробнее на таком исследовании, оно приводит к большому
богатству типов стационарных решений.
– закон сохранения
энергии системы. Полученные результаты позволяют полностью исследовать на
основании установленной механической аналогии стационарные решения модели (8).
Мы не останавливаемся подробнее на таком исследовании, оно приводит к большому
богатству типов стационарных решений.
В заключение ещё раз обратим внимание на
упомянутое выше преимущество использования аналогий с макродинамической моделью
(7). Если А = А(q) – неотрицательно
определённая и невырожденная матрица
при всех q Î Rn , то функционал (6) является невозрастающей
функцией времени на решениях q = q(x,
t) системы (7) (при надлежащих
краевых условиях, например, стационарных). Таким образом, функционал (6) играет
роль функции Ляпунова соответствующей динамической системы в функциональном
пространстве [15]. Это обстоятельство позволяет эффективно использовать второй
метод Ляпунова для исследования устойчивости стационарных решений системы (7).
Работа
выполнена при финансовой поддержке гранта
INTAS 97 – 30804.
Список литературы:
1.Уемов А.И. Аналогия в практике научных исследований. Из истории физико- математических наук. М.: Наука, 1970, 264 с.
2.Джемс Клерк Максвелл. Статьи и речи. М.: Наука, 1968, 422 с.
3.Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике (вып. 5). М.: Мир, 1977, 300 с.
4.Бутенин Н.В., Фуфаев Н.А. Введение в аналитическую механику. М.: Наука, 1991, 256 с.
5.Davydov A.S. Solitons and Energy Transfer Along Protein Molecules. // J. theor. Biol. 66 (1977), p. 379 – 387.
6.Пуанкаре А. Новые методы небесной механики. В 3–х т. Избр. тр. М.: Наука, т. 1, 1971, 771 с.; т. 2, 1972, 999 с.
7.Апонин Ю.М. Конфигурации особых точек вольтерровской системы трёх дифференциальных уравнений. НИВЦ АН СССР, 1982, 43 с. – Деп. в ВИНИТИ 13.07.82, № 3917 – 82.
8.Апонина Е.А., Апонин Ю.М., Базыкин А.Д. Анализ сложного динамического поведения в модели хищник – две жертвы. // Проблемы экологического мониторинга и моделирования экосистем, т. 5. – Л.: Гидрометеоиздат, 1982, стр. 163 – 180.
9.Андронов А.А. Математические проблемы теории автоколебаний. // В кн.: Первая Всесоюз. конф. по колебаниям. М.: Гостехтеориздат, 1933, т.1, стр. 32 – 71.
10.Басин М.А. Новые комплексные математические модели динамики живых систем. // В сб. Математика Компьютер Образование, вып. 8. Тезисы 8–ой Международной конференции. М.: Прогресс – Традиция, 2001, стр. 266.
11.Молчанов А.М. Нелинейности в биологии. Пущинский Научный Центр РАН. Пущино, 1992, 222 с.
12.Преснов Е.В., Малыгин С.Н. Аксиоматические модели феноменологической
термодинамики. В кн.: Термодинамика и кинетика биологических процессов. М.:
Наука, 1980, стр. 197 – 205.
13.Гледзер Е.Б., Должанский Ф.В., Обухов А.М. Системы гидродинамического
типа и их применение. М.: Наука, 1981, 366 с.
14.Свирежев Ю.М., Логофет Д.О. Устойчивость биологических сообществ. М.: Наука, 1978, 352 с.
15.Хенри Д. Геометрическая теория полулинейных параболических уравнений. М.: Мир, 1985, 376 с.
16.Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия. М.: Наука, 1979, 759 с.
17.Свирежев Ю.М. Нелинейные волны, диссипативные структуры и катастрофы в экологии. М.: Наука, 1987, 366 с.
18.Лоскутов А.Ю., Михайлов А.С. Введение в синергетику. М.: Наука, 1990, 271 с.
19.Кузнецов Ю. А., Бикташев В. Н., Апонина Е. А., Антоновский М. Я. Кросс–диффузионная модель динамики границы леса. // Проблемы экологического мониторинга и моделирования экосистем, т. 16. – Санкт-Петербург: Гидрометеоиздат, 1996, стр. 213 – 227.