ÌÎÄÅËÈÐÎÂÀÍÈÅ ÂÇÀÈÌÎÄÅÉÑÒÂÈß ÌÀÃÍÈÒÍÎÃÎ ÏÎËß Ñ ÎÁÚ¨ÌÍÛÌÈ ÂßÇÀÍÛÌÈ ÑÒÐÓÊÒÓÐÀÌÈ
Ñóñàê
È.Ï., Øèãàåâ À.Ñ., Ïîíîìàð¸â Î.À., Ôåñåíêî Å.Å.
(Ïóùèíî, Òîìñê)
Ïðåäñòàâëåí ìåõàíèçì âçàèìîäåéñòâèÿ ìàãíèòíîãî ïîëÿ
ñ æèäêîñòüþ. Â ðàìêàõ êîíöåïöèè ñîëèòîííîé ìîäåëè æèäêîñòè ïðåäëàãàåòñÿ
îáúÿñíåíèå ýôôåêòà ïàìÿòè â ñèñòåìàõ ñ âîäîðîäíûìè ñâÿçÿìè â ìàãíèòíîì ïîëå.
MODELING OF
INTERACTION MAGNETIC FIELD WITH BULK KNITTED STRUCTURES
Susak I.P.,
Shigaev A.S., Ponomarev O.A., Fesenko E.E.
(Pushchino, Tomsk)
A mechanism of interaction magnetic field with
liquid is presented. The memory effect in systems with hydrogenous bonds in
magnetic field within the framework of continual soliton concept of liquid
structure is also explained.
The behavior of hydrogen atoms in systems with
hydrogenous bonds plays an important role in transfer processes. It reveals a
number of fine non-linear and quantum effects. Suppose the structure of such
systems to be a bound band. The bands are tied by their edges between different
parts, which builds up a three dimensional net, a bulk knitted structure. DNA -
molecules, hydrogenous ferroelectrics, like triglycinsulphate and Rochelle
salt, tied polymeric balls of linear and quasilinear polymers [1 - 5],
fullerenes, kumulenes are all have these properties. There are data, that water
also belongs to such systems [6]. Electric and magnetic fields, as well as
electromagnetic radiation influence the position of phase transition points,
shifting the temperature and smearing out the transitions themselves [7]. Even
fields of 106 – 107 V/m change the properties of
narrow-band polymers (biomembranes) [8 - 10], being critical field values for
ferroelectrics or internal for membranes [11, 12].
Proton transition through a membrane may occur by
soliton mechanism through the chain of H-bonds in liquid water lining channels
(or in proteins, included in a membrane). It is known that the liquid structure
changes when is influenced by constant and alternate magnetic fields, these
changes being conserved during some tens of hours. These changes can be
identified by kinetic properties, for instance by change of viscosity, reaction
rate characteristics of dielectric relaxation spectra, IR -, UV - spectra and
luminescence. We suppose that the structure of the liquid under consideration
is defined by quantity of solitons on the band, between ties, soliton
concentration, and by concentration of ties in the system. We neglect the contributions of optical and
acoustic oscillations, assuming that more important role is played by rotation
of a band around its axis. We also neglect (in first approximation) serpentine
vibrations of a band. Usually a band has the length of approximately 20
sections. We will take into account molecular oscillations, taking out
different vibronic states. The aim of our analysis is to obtain an expression
for knitted liquid effective Hamiltonian, find out its connection with fluid
parameters, and external electric, magnetic, and electromagnetic fields.
We consider the liquid structure as a
three-dimensional surface composed in the following way. At temperature lower
than the critical one, the 3D-surface is supposed to transform into dipole
hexagonal structure such that dipole momenta of liquid molecules are arrange
according to the action minimum principle. We suppose that in liquid state the
amount of H-bonds per one molecule becomes less than 4.
The model is
characterized by the following parameters: molecular field energy, proportional
energy of hydrogen bonds ![]() kcal/mol 3D-surface transformation times, proportional to the
one H-bond lifetime for liquid
kcal/mol 3D-surface transformation times, proportional to the
one H-bond lifetime for liquid ![]() s [13-15], distances,
proportional to molecular size
s [13-15], distances,
proportional to molecular size ![]() m.
m.
The model takes into account the interaction of neighboring molecules as well as ones that far from each other bulk interaction. The three-dimensional structure is assumed to be with elasticity defined analogously to that in the theory of nematics. Structure transformations are associated with transformations of H-bonds, and we call each structure breach or disturbance a topological defect, which has a dimension, that can be fractional. Our model may be thought of as quasi-polymeric liquid. Several liquid molecules form band sections, that in turn are tied by their edges with the help of H-bonds. As a break of an H-bond occurs, the transformation of 3D-structure is coming. The sections of molecules change their orientation according to the action minimum principle, and then a retieing is taking place. So, the model describes isotropic medium, which has local anisotropy. The elasticity of segments composed of several molecules of liquid for longitudinal bends is considered to be equal to its average value, and is sufficiently big comparing to the elasticity for twist, analogously to the solid rod model. Quantitative description of the relation between these constants and their dependence on molecular length in frames of the theory of self - consistent field is presented in ref. [16].
Let our model be placed in external electromagnetic field. To
visualize electromagnetic field interaction on a segment of 3D-structure,
imagine it schematically as three oriented bands with many-colored edges for
determination of the direction of dipole momentum. We introduce dipole momentum
density distribution on a band. Transverse-oriented bands consist of segments,
built by molecules of the liquid. Instantaneous interaction of the edges of a
chain composed by oriented segments is assumed to be much weaker than the
interaction that builds the band itself. In the first approximation this
interaction is neglected, and the behavior of the band twisted in a ball is
considered. The system is placed into external electromagnetic field of low
intensity. In such system, solitons and breathers appear, which essentially
influence its properties. Let the direction of dipole momentum be from, say,
white edge of the band to the black one. The kink propagation on the segments of 3D-structure along the
band will turn it at angle ![]() , while breather propagation - at angle
, while breather propagation - at angle ![]() . Kinks and breathers propagate with velocities
. Kinks and breathers propagate with velocities ![]() and
and ![]() correspondingly.
Analytical form of breather and soliton type solutions of SG - equation is
described by the expressions
correspondingly.
Analytical form of breather and soliton type solutions of SG - equation is
described by the expressions ![]() and
and 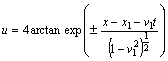 correspondingly.
During the interaction, a breather goes through a kink, undergoing a phase
shift. As the collisions are elastic, no any additional perturbation (like
"radiation") appears, and, secondly, the solutions can be found
analytically for all times with the help of, for instance, the inverse problem
method [17, 18]. We will not take into account their interaction. Consider the
case when there are no breathers. Then, the knitted system in the ground state
is described by the Hamiltonian
correspondingly.
During the interaction, a breather goes through a kink, undergoing a phase
shift. As the collisions are elastic, no any additional perturbation (like
"radiation") appears, and, secondly, the solutions can be found
analytically for all times with the help of, for instance, the inverse problem
method [17, 18]. We will not take into account their interaction. Consider the
case when there are no breathers. Then, the knitted system in the ground state
is described by the Hamiltonian
![]()
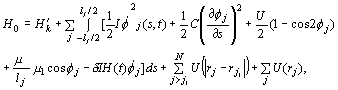 (1)
(1)
where
![]() - kinetic energy of
the system minus the kinetic energy related to collective coordinates of
solitons,
- kinetic energy of
the system minus the kinetic energy related to collective coordinates of
solitons, ![]() - rotation angle of a
twisting band on the segment between the points
- rotation angle of a
twisting band on the segment between the points ![]() and
and ![]() , which is of length
, which is of length ![]() , at the points
, at the points ![]() and
and ![]() the band is tied with
another one with a potential
the band is tied with
another one with a potential ![]() ,
, ![]() - the inertia
momentum density corresponding to the twist per unit length of the band,
- the inertia
momentum density corresponding to the twist per unit length of the band, ![]() - band's constant
elasticity,
- band's constant
elasticity, ![]() - density of
molecular field interaction energy,
- density of
molecular field interaction energy, ![]() - dipole momentum
density module,
- dipole momentum
density module, ![]() - the parameter of interaction of polymer chain with external magnetic
field
- the parameter of interaction of polymer chain with external magnetic
field ![]() .
.
Notice that the
points ![]() and
and ![]() are not tied with
each other. The dot over
are not tied with
each other. The dot over ![]() denotes time
derivative. The quantity
denotes time
derivative. The quantity ![]() is an external
potential acting on the point
is an external
potential acting on the point ![]() with coordinate
with coordinate ![]() , for instance, from a capillary. Suppose that, on the band's
segment between the points
, for instance, from a capillary. Suppose that, on the band's
segment between the points ![]() and
and ![]() there are
there are ![]() solitons (i.e. we
have an
solitons (i.e. we
have an ![]() - soliton solution).
Suppose also, that the concentration of solitons is not very high, so that we
may consider each soliton to be sufficiently distant from each other.
- soliton solution).
Suppose also, that the concentration of solitons is not very high, so that we
may consider each soliton to be sufficiently distant from each other.
Then
![]() (2)
(2)
where
![]() - single-soliton
solution [19], threaded on the band's segment between the points
- single-soliton
solution [19], threaded on the band's segment between the points ![]() and
and ![]() ,
, ![]() . Making use of (2) for the Hamiltonian (1) we have
. Making use of (2) for the Hamiltonian (1) we have
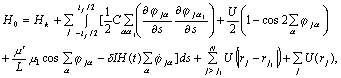 (3)
(3)
where
![]() - the total kinetic
energy of the system. The integration over s in (3) can be carried out explicitly,
which leads to the effective Hamiltonian describing the system in terms of free
particles, solitons and interactions between them. The Hamiltonian does not
depend on time, and, therefore may be calculated at any time. The simplest way
to do that is to chose
- the total kinetic
energy of the system. The integration over s in (3) can be carried out explicitly,
which leads to the effective Hamiltonian describing the system in terms of free
particles, solitons and interactions between them. The Hamiltonian does not
depend on time, and, therefore may be calculated at any time. The simplest way
to do that is to chose ![]() .
.
Now, let us
rewrite (3) in the form
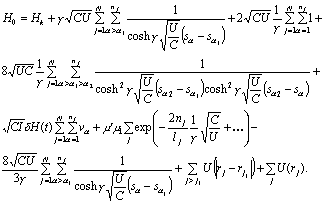 (4)
(4)
From now on we use
this effective Hamiltonian for the description of the system, which consists of
twisted bands between the points ![]() and
and ![]() and with the
positions of twirls on them in the points
and with the
positions of twirls on them in the points ![]() .
.
Describing liquid
as continuous medium, we conclude that the minimal energy in the model of liquid corresponds to the
absence of deformations in it. In liquid water, such state with minimal energy
or the ground state is the configuration with uniform orientation in the whole
bulk - hexagonal ice (Ih) for our model. Any deviation of director distribution
from uniform (i.e. the same in the whole bulk) is connected with the presence
of additional elastic energy in the model of liquid, that is may be
implemented only by external influence, connected, for example, with the
surfaces of a chosen segment, external electric and magnetic fields, etc. In
the absence of these influences or after the termination of their action, the
liquid tries to return to the state with uniform director orientation. In the
soliton model of liquid, when affected by external magnetic field, turnings of
certain band segments occur, which leads to the deviation of director
orientation distribution from uniform. There appears some addition to the free
energy (Gibbs' energy). Liquid in magnetic field has a state in which it can
remain for a long time ![]() , where
, where ![]() is hydrogen bond
lifetime. The system will continue to be in the state with this energy until an
external perturbation moves it to some other state, or until the temperature
changes. Thus, it is possible to describe the "memory" mechanism in
liquid water (MEW), including one-dimensional case for the soliton model. The addition to the free energy in the
soliton model of liquid is conditioned by soliton and breather concentrations.
They become apparent already at low values of magnetic field strength. This
addition changes the value of the specific heat of the liquid in magnetic
field:
is hydrogen bond
lifetime. The system will continue to be in the state with this energy until an
external perturbation moves it to some other state, or until the temperature
changes. Thus, it is possible to describe the "memory" mechanism in
liquid water (MEW), including one-dimensional case for the soliton model. The addition to the free energy in the
soliton model of liquid is conditioned by soliton and breather concentrations.
They become apparent already at low values of magnetic field strength. This
addition changes the value of the specific heat of the liquid in magnetic
field: ![]() ,
, ![]() - this is so called
configurational specific heat of the liquid [20]. It is characterized by the
amount of energy needed to change the configuration of chosen segments.
- this is so called
configurational specific heat of the liquid [20]. It is characterized by the
amount of energy needed to change the configuration of chosen segments.
It turned out that the knitted systems, those liquid water belongs to, have unique properties, that can be explained by the existence in them solitons and breathers. Many properties of water are explained in terms of continual soliton conception of water structure. Moreover, the structures of different knitted liquids under different magnetic fields can be described in terms of shift solitons and breathers. Soliton models provide good description of such systems.
References.
1.A.
Yu. Grosberg, A. R. Khokhlov Statistical
Physics of Macromolecules. M.: Nauka, 1989.
2.A.
Yu. Grosberg, A. R. Khokhlov About
Unsolved Problems of a Statistical Physics of Macromolecules.
Pushchino: Scientific Research Calculation
Center (NIVTs) AS USSR, 1985.
3.I.
M. Lifshits, A. Yu. Grosberg, A. R. Khokhlov, J. Uspekhi Fizicheskhix Nauk,
1979. 127, P. 353.
4.A.
Yu. Grosberg, A. R. Khokhlov, in the book: Solid - State Physics M.: Mir, 1989.
5.G.
Zundel Hydration and Intermolecular
Interactions. M.: Mir, 1972, 404 P.
6.S.
P. Gabuda Bound Water. The Facts and
Hypotheses. Novosibirsk: Nauka, 1982, 158 P.
7.O.
A. Ponomarev, I. P. Susak, in the Book: Diffusion assisted reactions. 2000, edited by A.I. Ivanov. - Volgograd, Russia 2000. P. 22.
8.V.
S. Bystrov, J. Critical Reviews in Biomedical Engineering, 2000, 3, P. 34-40.
9.A.
C. Angell, Water. A comprehensive treatise, ed. F. Franks. 7. - Plenum Press, 1982. – P. 1 - 81.
10.P.
M. Tomchuk, N. A. Protsenko, V. V. Krasnogolovets, J. Biological Membranes,
1984, 1, No 11, P. 1171-1178.
11.A.
G. Kalinichev, Reviews in Mineralogy and Geochemistry, 43, Mineralogical Society of America, Washington, D.C. 2001, edited by R.T. Cygan and J.D.
Kubicki. P. 83-130.
12.A.
K. Lyashenko, J. Critical Reviews in Biomedical Engineering, 1998, 2, P.
17-22.
13.O.
A. Ponomarev, E. E. Fesenko, J. Biophysics, 2000, 45, Pub. 3, P. 389-398.
14.O.
A. Ponomarev, I. P. Susak, in the book:
Recent Problems in Theoretical and Mathematical Physics. 2000, edited by
A.V. Aminova. - Kazan, Russia 2000. P.
72-78.
15.O.
A. Ponomarev, I. P. Susak, in the book: Recent Problems in Theoretical and
Mathematical Physics. 2001, edited by A.V.
Aminova. - Kazan, Russia 2001.
(in print).
16.H.
Gruler, Z. Naturforsh, A30, 230 (1975).
17.V.
E. Zakharov, S. V. Manakov, S. P. Novikov, L. P. Pitaevsky. The Theory of Solitons: Method of a Revertive Problem. M.:
Nauka, 1980.
18.R.
Dodd, J. Eilbek, J. Gibbon, Morris. Solitons
and Nonlinear Wave Equations. M.: Mir, 1988.
19.V.
E. Zakharov, L. A. Takhtadgyan, L. D. Faddeev. Doklady AN USSR. 219, No 6, 1974. P. 1334-1337.
20.Yu.
Ya. Efimov, Yu. I. Naberukhin, J. of Structural Chemistry. - 2000. 41, No 3. P. 532-539.