Горбань А. Н., Попова Т. Г., Садовский М. Г.
Институт вычислительного моделирования СО РАН, 660036 Красноярск; Институт биофизики СО РАН, 660036 Красноярск, Академгородок
В настоящее время число
расшифрованных нуклеотидных последовательностей (НП) возрастает
взрывообразно. Здесь возникает две проблемы: проблема поиска и
установления порядка во множестве генетических текстов, и проблема
выделения тех участков в НП, которые отличаются между собой своими
свойствами, функциональным значением, либо историей. Отметим,
что порядок на множестве НП может быть задан несколькими различными
способами. Во-первых, порядок определяется таксономическим положением
носителей (видов) тех или иных НП; во-вторых, порядок может определяться
в соответствии с близостью функций, кодируемых различными НП.
Наконец, в-третьих, порядок на множестве НП может быть задан с
помощью их классификации по статистическим свойствам самих НП
только, без привлечения какой-либо дополнительной информации.Для
построения такой классификации сопоставим каждой НП её частотный
словарь (ЧС) - множество всех слов (подпоследовательностей) заданной
длины
q (его толщина), встречающихся в изучаемой НП, вместе
с указанием их частот [1]. Тогда каждой НП из изучаемого множества
можно (однозначно) сопоставить её ЧС, а этому последнему - точку
в 4
q-мерном
пространстве. Далее, необходимо все эти точки разбить на некоторое
число классов. Для построения такой классификации нами использовался
метод автоматической классификации - метод динамических ядер,
а расстояние между точками в пространстве определялось как евклидово
расстояние. Следует отметить, что для ЧС различной толщины мы
получаем, в общем случае, различные классификации. Построение
классификации, кроме того, зависит от использованного условия
различимости получающихся классов. Мы строили автоматические классификации
нуклеотидных последовательностей (НП) генов
Ca-зависимых
белков и НП 16SРНК. Построенные классификации коррелировали как
с функциональной, так и с таксономической классификациями, независимо
существующими на множестве изучаемых НП. При построении описанной
выше классификации центр класса (ядро) и расстояния от ЧС до ядра
определялись с помощью евклидова расстояния, где координатами
точек являлись частоты
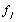 :
:
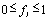 ,
, 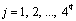 соответствующих слов. Упорядоченность следования нуклеотидов НП
проявляется в неслучайности их взаимного расположения. В каждом
ЧС толщины q содержится вся информация о ЧС толщины на
единицу меньшей; обратное в общем случае неверно. Предложен способ
восстановления ЧС, основанный на принципе максимума энтропии восстановленного
ЧС. Таким образом, восстановленный ЧС обладает максимальной возможной
неопределённостью; что позволяет существенно усилить построение
классификации. Для выделения эффекта неслучайности в построении
автоматической классификации перейдём при её построении от частот
слов к отношениям реальных частот данного слова и его восстановленной
частоты (по словарям меньшей толщины):
соответствующих слов. Упорядоченность следования нуклеотидов НП
проявляется в неслучайности их взаимного расположения. В каждом
ЧС толщины q содержится вся информация о ЧС толщины на
единицу меньшей; обратное в общем случае неверно. Предложен способ
восстановления ЧС, основанный на принципе максимума энтропии восстановленного
ЧС. Таким образом, восстановленный ЧС обладает максимальной возможной
неопределённостью; что позволяет существенно усилить построение
классификации. Для выделения эффекта неслучайности в построении
автоматической классификации перейдём при её построении от частот
слов к отношениям реальных частот данного слова и его восстановленной
частоты (по словарям меньшей толщины): 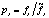 и
и 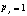 , если
, если 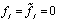 . Построение
автоматической классификации по такому отношению позволит выделить
вклад неслучайности во взаимном расположении нуклеотидов в построение
классификации. Предварительные результаты построения автоматической
классификации по отношениям частот, проведённые на множестве НП
16SРНК, показали ряд отличий от случая классификации, построенной
только по реальным частотам слов в ЧС этих НП. Важнейшее отличие
заключается в нарушении следующего правила монотонности, справедливого
для классификаций по реальным ЧС: если на длине слов q1
классификация не строится, то она не будет строится и на любой
другой длине слов q2 > q1.
Если для реальных частот автоматическая классификация давала разбиение
множества НП 16SРНК на семь классов на длине слов 2, и разбиение
на два класса - на длине слов 3, то для случая классификации по
отношениям частот на длине слов 2 хорошего разбиения на классы
не возникало, в то время, как такая классификация на длине слов
3 имела более тонкую структуру; более того, в отличие от классификации
по реальным частотам, НП классифицировались и на длине слов 4
по отношениям частот.
. Построение
автоматической классификации по такому отношению позволит выделить
вклад неслучайности во взаимном расположении нуклеотидов в построение
классификации. Предварительные результаты построения автоматической
классификации по отношениям частот, проведённые на множестве НП
16SРНК, показали ряд отличий от случая классификации, построенной
только по реальным частотам слов в ЧС этих НП. Важнейшее отличие
заключается в нарушении следующего правила монотонности, справедливого
для классификаций по реальным ЧС: если на длине слов q1
классификация не строится, то она не будет строится и на любой
другой длине слов q2 > q1.
Если для реальных частот автоматическая классификация давала разбиение
множества НП 16SРНК на семь классов на длине слов 2, и разбиение
на два класса - на длине слов 3, то для случая классификации по
отношениям частот на длине слов 2 хорошего разбиения на классы
не возникало, в то время, как такая классификация на длине слов
3 имела более тонкую структуру; более того, в отличие от классификации
по реальным частотам, НП классифицировались и на длине слов 4
по отношениям частот.
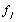 :
:
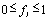 ,
, 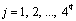 соответствующих слов. Упорядоченность следования нуклеотидов НП
проявляется в неслучайности их взаимного расположения. В каждом
ЧС толщины q содержится вся информация о ЧС толщины на
единицу меньшей; обратное в общем случае неверно. Предложен способ
восстановления ЧС, основанный на принципе максимума энтропии восстановленного
ЧС. Таким образом, восстановленный ЧС обладает максимальной возможной
неопределённостью; что позволяет существенно усилить построение
классификации. Для выделения эффекта неслучайности в построении
автоматической классификации перейдём при её построении от частот
слов к отношениям реальных частот данного слова и его восстановленной
частоты (по словарям меньшей толщины):
соответствующих слов. Упорядоченность следования нуклеотидов НП
проявляется в неслучайности их взаимного расположения. В каждом
ЧС толщины q содержится вся информация о ЧС толщины на
единицу меньшей; обратное в общем случае неверно. Предложен способ
восстановления ЧС, основанный на принципе максимума энтропии восстановленного
ЧС. Таким образом, восстановленный ЧС обладает максимальной возможной
неопределённостью; что позволяет существенно усилить построение
классификации. Для выделения эффекта неслучайности в построении
автоматической классификации перейдём при её построении от частот
слов к отношениям реальных частот данного слова и его восстановленной
частоты (по словарям меньшей толщины): 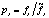 и
и 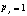 , если
, если 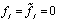 . Построение
автоматической классификации по такому отношению позволит выделить
вклад неслучайности во взаимном расположении нуклеотидов в построение
классификации. Предварительные результаты построения автоматической
классификации по отношениям частот, проведённые на множестве НП
16SРНК, показали ряд отличий от случая классификации, построенной
только по реальным частотам слов в ЧС этих НП. Важнейшее отличие
заключается в нарушении следующего правила монотонности, справедливого
для классификаций по реальным ЧС: если на длине слов q1
классификация не строится, то она не будет строится и на любой
другой длине слов q2 > q1.
Если для реальных частот автоматическая классификация давала разбиение
множества НП 16SРНК на семь классов на длине слов 2, и разбиение
на два класса - на длине слов 3, то для случая классификации по
отношениям частот на длине слов 2 хорошего разбиения на классы
не возникало, в то время, как такая классификация на длине слов
3 имела более тонкую структуру; более того, в отличие от классификации
по реальным частотам, НП классифицировались и на длине слов 4
по отношениям частот.
. Построение
автоматической классификации по такому отношению позволит выделить
вклад неслучайности во взаимном расположении нуклеотидов в построение
классификации. Предварительные результаты построения автоматической
классификации по отношениям частот, проведённые на множестве НП
16SРНК, показали ряд отличий от случая классификации, построенной
только по реальным частотам слов в ЧС этих НП. Важнейшее отличие
заключается в нарушении следующего правила монотонности, справедливого
для классификаций по реальным ЧС: если на длине слов q1
классификация не строится, то она не будет строится и на любой
другой длине слов q2 > q1.
Если для реальных частот автоматическая классификация давала разбиение
множества НП 16SРНК на семь классов на длине слов 2, и разбиение
на два класса - на длине слов 3, то для случая классификации по
отношениям частот на длине слов 2 хорошего разбиения на классы
не возникало, в то время, как такая классификация на длине слов
3 имела более тонкую структуру; более того, в отличие от классификации
по реальным частотам, НП классифицировались и на длине слов 4
по отношениям частот.