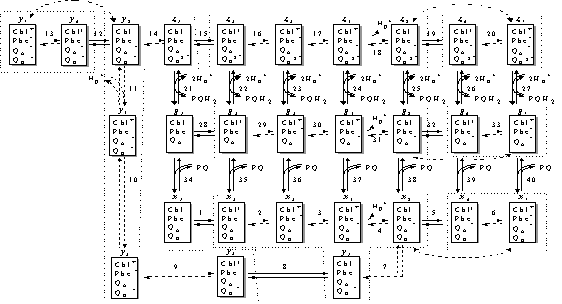
После длительной темновой
адаптации P680 полностью восстанавливается, а феофитин и QA,
напротив, переходят в окисленное состояние. Следовательно, перед включением
света ФС2 может находится только в двух состояниях, x1 и g1,
между которыми устанавливается равновесие (реакция 34). Равновесные
концентрации этих состояний полностью определяются константой связывания и
суммарной концентрацией пластохинона, PQ, в мембране.
После включения освещения
P680 переходит в возбужденное состояние, x2 и g2 (реакции
1 и 28, соответственно), с последующей передачей электрона на феофитин (реакции
2 и 29), то есть происходит первичное разделение зарядов. Так как электрон не
может стабилизироваться на феофитине, то происходит его дальнейшая передача на
QA (реакции 3 и 30). Далее, система расщепления воды ( СРВ )
донирует электрон окисленному пигменту, приводя его в первоначальное (т.е.
восстановленное и невозбужденное) состояние x5 и g5.
Каждые четыре акта восстановления окисленного P680 комплексом СРВ сопровождаются
поглощением двух молекул H2O, выделением одной молекулы
молекулярного кислорода и четырех протонов,  во внутритилакоидное пространство, которое
при этом заряжается положительно. В нашей модели мы не рассматривали
молекулярный механизм функционирования СРВ, а предположили, что на каждый
электрон, переданный от СРВ на окисленный P680, во внутритилакоидное
пространство выделяется один протон (реакции 4 и 31). Таким образом,
последовательность стадий (1-4) или (28-31) приводит к образованию так называемых
«закрытых» реакционных центров (РЦ) с восстановленным QA. Дальнейшее
освещение закрытых РЦ может приводить к повторному возбуждению пигмента
(реакции 5 и 32) и первичному разделению зарядов (реакции 6 и 33). В результате
этих процессов образуются состояния ФС2 с окисленным пигментом и
восстановленными феофитином и QA, т. е. x7 и g7,
которые являются высокоэнергетическими. Нестабильный заряд на феофитине может
рекомбинировать с электронной дыркой на Р680+ двумя способами: либо
приводя к репопуляции возбужденных состояний Р680* (переход состояний с
индексом 7 в состояния с индексом 6), либо непосредственно в основное
состояние, путем безызлучательной рекомбинации первичной пары (переход
состояний с индексом 7 в состояния с индексом 5 изображен на схеме пунктирными
стрелками без номера). В настоящее время нет единого мнения о том, какой из
этих путей действительно реализуется [8].
во внутритилакоидное пространство, которое
при этом заряжается положительно. В нашей модели мы не рассматривали
молекулярный механизм функционирования СРВ, а предположили, что на каждый
электрон, переданный от СРВ на окисленный P680, во внутритилакоидное
пространство выделяется один протон (реакции 4 и 31). Таким образом,
последовательность стадий (1-4) или (28-31) приводит к образованию так называемых
«закрытых» реакционных центров (РЦ) с восстановленным QA. Дальнейшее
освещение закрытых РЦ может приводить к повторному возбуждению пигмента
(реакции 5 и 32) и первичному разделению зарядов (реакции 6 и 33). В результате
этих процессов образуются состояния ФС2 с окисленным пигментом и
восстановленными феофитином и QA, т. е. x7 и g7,
которые являются высокоэнергетическими. Нестабильный заряд на феофитине может
рекомбинировать с электронной дыркой на Р680+ двумя способами: либо
приводя к репопуляции возбужденных состояний Р680* (переход состояний с
индексом 7 в состояния с индексом 6), либо непосредственно в основное
состояние, путем безызлучательной рекомбинации первичной пары (переход
состояний с индексом 7 в состояния с индексом 5 изображен на схеме пунктирными
стрелками без номера). В настоящее время нет единого мнения о том, какой из
этих путей действительно реализуется [8].
В любом из состояний gi,
i=1,...7, может происходить связывание пластохинона с QB центром ФС2
(реакции 34 – 40) с образованием соответствующих состояний xi,
i=1,...7. Связанный пластохинон является двухэлектронным переносчиком и,
следовательно, может последовательно акцептировать два электрона, пришедшие на
QA (перенос первого электрона с  на QB описывается реакцией 7). Реакция
14 соответствует переносу электрона с
на QB описывается реакцией 7). Реакция
14 соответствует переносу электрона с  на семихинон, расположенный в сайте QB
с образованием полностью депротонированного пластохинола,
на семихинон, расположенный в сайте QB
с образованием полностью депротонированного пластохинола, 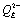 .
Далее, под действием света в ФС2, в QB сайте которой связан
депротонированный пластохинол (соответствующие состояния ФС2 обозначены буквами
zi, i=1,...7) происходит уже описанная выше последовательность
событий, приводящая к восстановлению QA (реакции 15 – 20). Наряду с
этим, в каждом из состояний zi, i=1,...7, может происходить
высвобождение пластохинола с предварительным поглощением двух протонов,
.
Далее, под действием света в ФС2, в QB сайте которой связан
депротонированный пластохинол (соответствующие состояния ФС2 обозначены буквами
zi, i=1,...7) происходит уже описанная выше последовательность
событий, приводящая к восстановлению QA (реакции 15 – 20). Наряду с
этим, в каждом из состояний zi, i=1,...7, может происходить
высвобождение пластохинола с предварительным поглощением двух протонов, 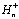 ,
из стромы хлоропласта (которая при этом заряжается отрицательно) и образованием
первоначальных состояний gi, i=1,...7, с пустым сайтом QB (реакции
21-27), что и замыкает каталитический цикл фотосистемы 2.
,
из стромы хлоропласта (которая при этом заряжается отрицательно) и образованием
первоначальных состояний gi, i=1,...7, с пустым сайтом QB (реакции
21-27), что и замыкает каталитический цикл фотосистемы 2.
Величины xi, yi,
zi, gi, i=1,...7, являются переменными модели, то есть
определяются системой дифференциальных уравнений типа :
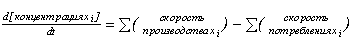 (1),
(1),
соответствующей схеме каталитического цикла ФС2, изображенной на рис. 1.
Концентрации протонов во внутритилакоидном пространстве, 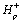 ,
строме хлоропласта,
,
строме хлоропласта, 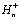 ,
разность электрических потенциалов на мембране тилакоида, DY, а также внутримембранные
концентрации пластохинона и пластохинола являются параметрами модели. Скорости
всех реакций задаются с помощью закона действующих масс и являются функциями
переменных и параметров модели. Для полного описания каждой реакции достаточно
знать ее константу равновесия и константу скорости обратной реакции. При
заданном конкретном значении константы равновесия Keqi, константа скорости прямой
реакций (ki) выражается через константу скорости обратной реакции (k-i)
следующим образом:
,
разность электрических потенциалов на мембране тилакоида, DY, а также внутримембранные
концентрации пластохинона и пластохинола являются параметрами модели. Скорости
всех реакций задаются с помощью закона действующих масс и являются функциями
переменных и параметров модели. Для полного описания каждой реакции достаточно
знать ее константу равновесия и константу скорости обратной реакции. При
заданном конкретном значении константы равновесия Keqi, константа скорости прямой
реакций (ki) выражается через константу скорости обратной реакции (k-i)
следующим образом:
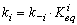 (2)
(2)
Константы равновесия
окислительно-восстановительных реакций определяются из экспериментально
полученных данных по среднеточечным редокс потенциалам.
Стадии 1, 5, 8, 12, 15, 19,
28 и 32 являются световыми и описывают процесс перехода Chl в
возбужденное состояние Chl* (константы 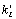 ,
i=1,5,8,12,15,19,28,32) и обратный ему процесс дезактивации возбужденного
состояния (константы ci, i=1,5,8,12,15,19,28,32).
Константы
,
i=1,5,8,12,15,19,28,32) и обратный ему процесс дезактивации возбужденного
состояния (константы ci, i=1,5,8,12,15,19,28,32).
Константы 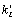 пропорциональны интенсивности света [4]:
(
пропорциональны интенсивности света [4]:
(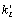 ~ I×s, где I – интенсивность
света, s – поперечное сечение
поглощения ФС2.). В частности, при отсутствии освещения, все эти константы
равны нулю. Дезактивация возбужденных состояний Chl* сопровождается излучением
флуоресценции (хотя возможны и другие пути дезактивации, в нашей работе не
рассматриваемые).
~ I×s, где I – интенсивность
света, s – поперечное сечение
поглощения ФС2.). В частности, при отсутствии освещения, все эти константы
равны нулю. Дезактивация возбужденных состояний Chl* сопровождается излучением
флуоресценции (хотя возможны и другие пути дезактивации, в нашей работе не
рассматриваемые).
В рамках нашей модели функция
для расчета величины флуоресценции была представлена в виде суммы концентраций
флуоресцирующих состояний ФС2 (то есть состояний с возбужденным Chl),
умноженных на соответствующие им константы флуоресценции ci:
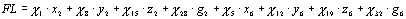 (3)
(3)
Любая стадия, включающая
перенос электрического заряда через мембрану, продуцирует мембранный потенциал
(DY), который, в свою очередь,
влияет на константу равновесия и константы скоростей всех электрогенных стадий
[5, 6, 7]:
Keq(DY)=exp(-a×DY/(RT/F))×Keq,
k+(DY)=exp(-d×a×DY/(RT/F))×k+, (4)
k–(DY)=exp((1-d)×a×DY/(RT/F))×k– .
Здесь a×DY – тот мембранный потенциал,
который генерируется рассматриваемой стадией при переносе заряда через
мембрану, d – та часть мембранного
потенциала (a×DY),
которая влияет на константу скорости прямой реакции.
Редуцированная математическая модель. В предыдущем подразделе мы построили полную
математическую модель ФС2 (рис. 1). Все процессы, изображенные на этом рисунке
могут быть условно разделены на быстрые (с характерным временем менее 100
мксек) и медленные (с характерным временем не менее 1 мсек). К медленным
реакциям относятся все световые стадии перехода P680 в возбужденное состояние
(реакции 1, 5, 8, 12, 15, 19, 28, 32), а также связывание пластохинона (реакции
34 – 40) и диссоциации пластохинола (реакции 21 – 27). Все остальные реакции
являются быстрыми. Таким образом, возникает возможность проведения редукции
быстрых процессов в полной математической модели ФС2.
Перейдя к пределу по
константам скоростей быстрых реакций, делая замену переменных:
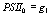 ,
, 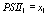 ,
,
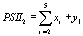 ,
, 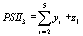 , (5)
, (5)
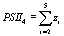 ,
, 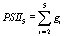
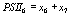 ,
, 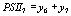 ,
, 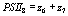 ,
, 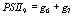 ,
,
выражая старые переменные через новые, приходим к
системе дифференциальных уравнений для новых «медленных» переменных. На схеме
рис.1. замкнутыми пунктирными линиями показаны состояния ФС2, сгруппированные
проведенной редукцией в новые переменные согласно преобразованиям (5).
Полностью процесс получения
редуцированной системы дифференциальных уравнений приведен в работе [9].
Численное решение системы
дифференциальных уравнений производилось с помощью пакета SCAMP. Была
разработана исследовательская среда (Borland C++ 4.0, Windows95), которая: (1)
накапливала численные решения, полученные в пакете SCAMP, (2) позволяла
модифицировать параметры исследуемой модели перед очередным расчетом, (3)
выводила данные, накопленные в результате расчетов при изменяемых параметрах, в
виде графических зависимостей на экран. При выводе на экран кинетических
зависимостей использован логарифмический масштаб времени.
Результаты и обсуждение.
Разработанную модель мы
применили к описанию одного из широко известных эксперментальных феноменов –
кривой индукции флуореценции хлорофилла, которая представляет собой увеличение
интенсивности флуоресценции объекта в ответ на включение освещения после
периода темновой адаптации. Особенности кинетики индукции флуоресценции зеленых
растений хорошо изучены, например, в работах [10,11]. Наиболее характерным
участком индукционной кривой является так называемая быстрая фаза (OIDP –
участок) – увеличение выхода флуоресценции до максимального значения за времена
порядка нескольких секунд. Согласно современным представлениям, ее отдельные
кинетические компоненты соответствуют протеканию различных процессов в
фотосинтетическом аппарате растения [12] : увеличению концентрации
восстановленного QA, возрастанию электрического потенциала на
мембране тилакоида, изменению редокс состояния пластохинонового пула и т.п.
Одной из главных целей нашей
работы была проверка гипотезы о возможности объяснить наблюдаемую в
эксперментах немонотонность OIDP кинетики, опираясь
исключительно на регуляторные свойства самой фотосистемы 2. Мы попытались
выяснить, может ли кривая индукции флуоресценции, построенная на основе нашей
модели, иметь в диапазоне 10-500 мсек характерную немонотонность: локальный
минимум или по крайней мере «плечо», которые наблюдаются на экспериментально
полученных кривых [10, 11]. Для этого мы исследовали модельные кривые индукции
флуоресценции при разных значениях параметров модели.
Результаты моделирования
показали, что при различных значениях параметров модели кривая индукции
флуоресценции всегда имеет характерную S-образную форму (рис. 2). Никакого
локального минимума или «плеча» на этапе быстрого возрастания флоуресценции не
наблюдается. Варьирование параметров модели ведет лишь к изменению
стационарного уровня флуоресценции и, в ряде случаев, к изменению скорости его
достижения.
Так, увеличение световой
константы kL, повышает стационарное значение флуоресценции и
сокращает время, за которое оно достигается (рис. 2а). Напротив, закисление
стромы и внутритилакоидного пространства, которое приводит к отклонению от
нормальной разности протонного градиента, DpH, равного 2 (pHn =8,
pHp =6) обусловливает снижение стационарного уровня
флуоресценции (рис. 2 б).
Результаты проведенного нами
исследования позволяют сделать вывод о том, что наблюдаемые на начальном
участке индукционной кривой эффекты немонотонности не являются прямым
следствием процессов, протекающих внутри комплекса фотосистемы 2. Происхождение
этих эффектов, по всей видимости, следует искать во взаимодействии ФС2 с
другими первичными процессами фотосинтеза – генерацией электрохимического
потенциала на мембране тилакоида и сопутствующими ей трансмембранными ионными
потоками. Имеются данные, что выход флуоресценции в быстрой фазе индукции
флуоресценции может зависеть от редокс-состояния пула пластохинонов [10,11].
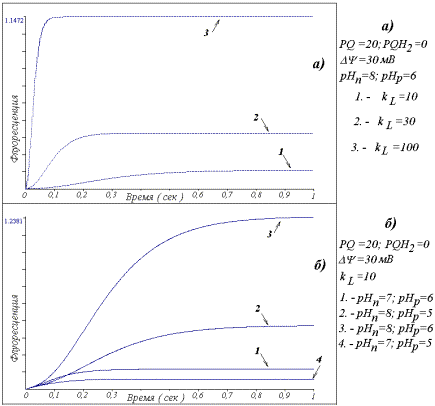
Рис. 2. Индукция
флуоресценции, рассчитанная в модели ФС2. (а)При
изменении интенсивности светового возбуждения: (1) kL =10, (2)kL
=30, (3)kL =100. (б)Для
различных рН стромы (pHn) и люмена (pHp) тилакоида: (1)рHn =7,
pHp =6, (2)рHn=8, pHp=5, (3)рHn=8,
pHp=6, (4)рHn=7, pHp=5. Указаны параметры
модели, неизменные для каждого расчета.
В настоящее время
продолжается построение и исследование модели тилакоида, объединяющей
функциональные блоки, соответствующие молекулярным комплексам, а также
подвижным переносчикам электронов, включенным в процесс трансформации энергии
световых стадий фотосинтеза: описанная выше модель ФС2, цитохромный комплекс b6f,
пул плаcтохинолов, подвижный переносчик пластоцианин, фотосистема 1, комплекс
АТФ-синтетазы, ионные каналы, осуществляющие перенос H+, K+, Cl+ через мембрану тилакоида.
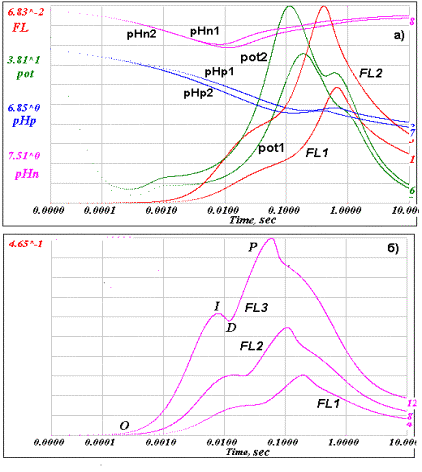
Рис.3. Кинетический ответ
модели тилакоида в логарифмическом масштабе времени. (а) Для двух значений интенсивности светового возбуждения (kL(1)=8,
и kL(2)=16) представлены : кривые индукции флуоресценции FL1 и FL2,
изменение во времени электрического потенциала pot1 и pot2, и изменение рН
(люмен – рНр1 и рНр2, строма – рНn1 и рНn2 ). (б) Кривые индукции флуоресценции FL1, FL2 и FL3 для трех значений
интенсивности светового возбуждения (kL(1)=20, kL(2)=40 и
kL(3)=80). На кривой FL3 даны обозначения характерных фаз
OIDP-кинетики.
На рис. 3 приведены
результаты расчета кинетического ответа модели тилакоида на ступенчатое
включение постоянного света после темновой адаптации. Рис. 3а показывает
одновременно как индукцию флуоресценции (кривые FL1 и FL2), так и изменение
величины трансмембранного электрохимического потенциала. Величина
электрического потенциала (DY)
отражает распределение объемного заряда в компартментах люмена и стромы
тилакоида и описывается кривыми pot1 и pot2 . Изменения концентрации ионов
водорода в люмене и строме определяются кривыми изменения рН (люмен – рНр1 и
рНр2, строма – рНn1 и рНn2 ).
На рис. 3б показан
результат расчета для модели тилакоида индукции флуоресценции в широком
диапазоне световых констант. Такой компьютерный эксперимент позволяет подойти к
моделированию эффектов светового насыщения индукции флуоресценции,
экспериментально исследованных в [10, 11].
Результаты компьютерных
экспериментов на более полной модели фотосинтетических процессов, включающей
модель ФС2, как один из блоков, позволяют описать индукционные кривые с
характерной немотонной OIDP-кинетикой. Как было показано выше, это невозможно в
рамках модели изолированной ФС2.
Разрабатываемая нами модель
дает возможность анализировать взаимосвязь и взаимовлияние потоков энергии и
вещества в первичных процессах фотосинтеза.
Литература.
1. Baake E., Shloeder J.P. –
1992. Bull. Math. Biol. 54. – Р.999-1021
2. Renger G. and Shulze A. Photobiochem. Photobiophys. 9. – 1985. – Р.79-87.
3. Trissl H.-W., Gao Y. And Wulf K. – 1993. Biophys.J. 64. – Р.974-988.
4.
Молекулярные
механизмы трансформации энергии в первичных процессах фотосинтеза // Итоги
науки и техники, сер. Биофизика. – 1987. – Т.20.
5.
Демин
О.В., Вестерхофф Х.В., Холоденко Б.Н. Биохимия 63. – 1998. – Р.755-772.
6.
Скулачев В.П.,
Козлов И.А. Протонные аденозинтрифосфатазы: молекулярные биологические
генераторы тока. – М.: Наука, 1977.
7. Reynolds I.A., Johnson E.A. and Tanford C. – 1985. Proc. Natl. Acad.
Sci. USA. 82. – Р.6869-6873.
8. Leibl W., Breton J., Deprez J. and Trissl H.W. – 1989. Photosynth. Res.
22. – Р.257-275.
9.
Лебедева Г.В.,
Беляева Н.Е., Ризниченко Г.Ю., Рубин А.Б., Демин О.В.
Кинетическая модель фотосистемы II высших растений // Физ. химия, в печати.
10. Neubauer C., Schreiber U. Z. Naturforsch. – 1987. 42. Р.1246-1254.
11. Strasser R.J., Srivastava A. Govindjee (1995). Photochemistry and
photobiology. 61. – No 1. – Р. 32 – 42.
12. Dau H. – 1994. J.Photochem. Photobiol. B: Biology 26. – Р.3-27.
13.
Принципы
регуляции и модельные системы первичных процессов фотосинтеза // Итоги науки и
техники, сер. Биофизика. – 1987. – Т.22.
14.
Кукушкин
А.К., Караваев В.А. Теоретические исследование процессов миграции энергии и
электронного транспорта в фотосинтезе высших растений // Биофизика. – 1979. –
Т.24. – Вып. 1. – С.92-95.
15.
Ризниченко
Г.Ю. Математические модели первичных процессов фотосинтеза. Итоги науки и
техники, сер. Биофизика. – 1991. – Т.31.
![]() ,
который затем используется для синтеза АТФ.
,
который затем используется для синтеза АТФ.