Термостаты.

Часто взаимодействие с тепловым резервуаром моделируется дополнительной силой трения . Коэффициент l выбирается таким образом, чтобы сила обеспечила изменение энергии системы по закону

Здесь E – энергия изолированной системы (при отсутствии взаимодействия с резервуаром сохраняется), t _E – характерное время взаимодействия с резервуаром, – кинетическая энергия системы, – константа, равная средней кинетической энергии, соответствующей температуре резервуара T₀. Уравнения движения метода имеют вид

a =1,…,N

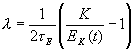
Расчёт траекторий движения в молекулярной динамике по этим уравнениям носит название WCEB (weak coupling to an external bath). Однако, среди специалистов такой метод задания теплового резервуара более известен как метод термостата Берендсена. Этот метод широко применяется для моделирования молекулярной динамики молекул с большим числом степеней свободы, в частности полипептидов и белков.

В броуновской динамике сила, осуществляющая взаимодействие системы с тепловым резервуаром, состоит из двух частей: систематической силы трения F_T и шума F_C.

i=1,…,3N

h _i – коэффициент трения, соответствующий координате Xⁱ. Сила F_C(t) – d -коррелированный по времени, гауссовский случайный процесс. Первый и второй моменты этого процесса равны

Интенсивность шума D_ij называют тензором диффузии. Уравнения движения метода броуновской динамики называются уравнениями Ланжевена, а метод расчёта молекулярной динамики по этим уравнениям - методом Ланжевеновской динамики

i=1,…,3N

Добавление случайной силы превращает все динамические переменные в случайные величины. Меняется сам способ описания состояния системы: бессмысленно говорить о нахождении системы в точке фазового пространства. Теперь под состоянием системы понимается плотность распределения P(X,V,t) на фазовом пространстве: P(X,V,t) dX dV равно вероятности нахождения системы в момент времени t в малой окрестности точки (X,V). С вышеуказанным уравнением связано дифференциальное уравнение второго порядка для функции P(X,V,t) – уравнение Фоккера-Планка.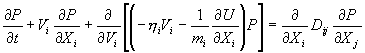

Это уравнение описывает эволюцию состояния нашей системы. При выполнении этих условий, любое начальное состояние P₀(X,V) будет стремиться к единственному стационарному состоянию P? (X,V). Естественно потребовать, чтобы это стационарное состояние совпадало с равновесным ансамблем Гиббса, плотность распределения которого равна

где H(X,V) – гамильтониан системы. Достаточное условие того, чтобы распределение b было стационарным решением уравнения Фоккера-Планка, суть соотношение

Следовательно, интенсивность шума в броуновской динамике не произвольна, а должна выбираться в соответствии с этим уравнением.

В методе Андерсона (МА) взаимодействие системы с тепловым резервуаром моделируется следующим образом. В определённые моменты времени t_k движения изолированной системы происходит замена её скоростей V на новые скорости U. Скорости U суть случайные величины, распределённые в соответствии с импульсной частью P_M(X,V) равновесного распределения Гиббса. Если на систему не наложено геометрических связей, то P_M(X,V) не зависит от X и совпадает с распределением Максвелла.

Если система состоит из одной частицы массы m, то предлагаемая замена скоростей эквивалентна соударению с виртуальным атомом резервуара, который имеет ту же массу m и скорость U, выбранную случайно из распределения Максвелла. Но если частица обладает внутренними степенями свободы, то предлагаемая замена не эквивалентна одному соударению.

Метод Нозе. Во всех предыдущих методах, моделирующих динамику системы в тепловом резервуаре, тепловой резервуар явно не описывался. Обычно вводится явно дополнительная степень свободы s, которая описывает резервуар. Лагранжиан расширенной системы имеет вид

Здесь Q – некоторая константа. Из уравнений Лагранжа получаются уравнения движения как для атомов системы, так и для переменной s. Хотя физический смысл переменной s не ясен, было показано, что такое искусственное расширение системы формально позволяет оценивать средние по Гиббсу величины от функций, определённых на фазовом пространстве системы (без резервуара), путём усреднения их вдоль траекторий расширенной системы.

Часто изучаемые процессы происходят в локализованной области. Например, в ферментативных реакциях, при связывании лигандов для транспортировки. В этих случаях биологическая активность связана с динамикой в окрестности активного центра или места связывания. Для моделирования таких процессов наиболее широко используется метод МД со стохастическими граничными условиями (СГУ). В этом методе изучаемая система разделяется на две области: «реакционную» зону (РЗ) и резервуарную область (РО). Реакционная зона содержит ту часть системы, которая участвует в интересуемом нас процессе. Резервуарная область исключается из вычислений и её влияние на атомы в РЗ учитывается эффективно через среднюю силу и стохастическую силу. Причём стохастическая сила действует только на атомы в окрестности границы РЗ, которая называется буферной зоной.

Движение атомов в реакционной зоне находятся путём решения следующих уравнений

, в РЗ

, в буферной зоне

Здесь – это потенциал взаимодействия в вакууме. Стохастическая сила , осуществляющая взаимодействие с резервуарной областью, традиционно выбирается в форме силы Ланжевена. Возможны и другие способы взаимодействия с резервуаром (см. предыдущие методы). Что касается выбора средней силы, то тут общих правил нет.

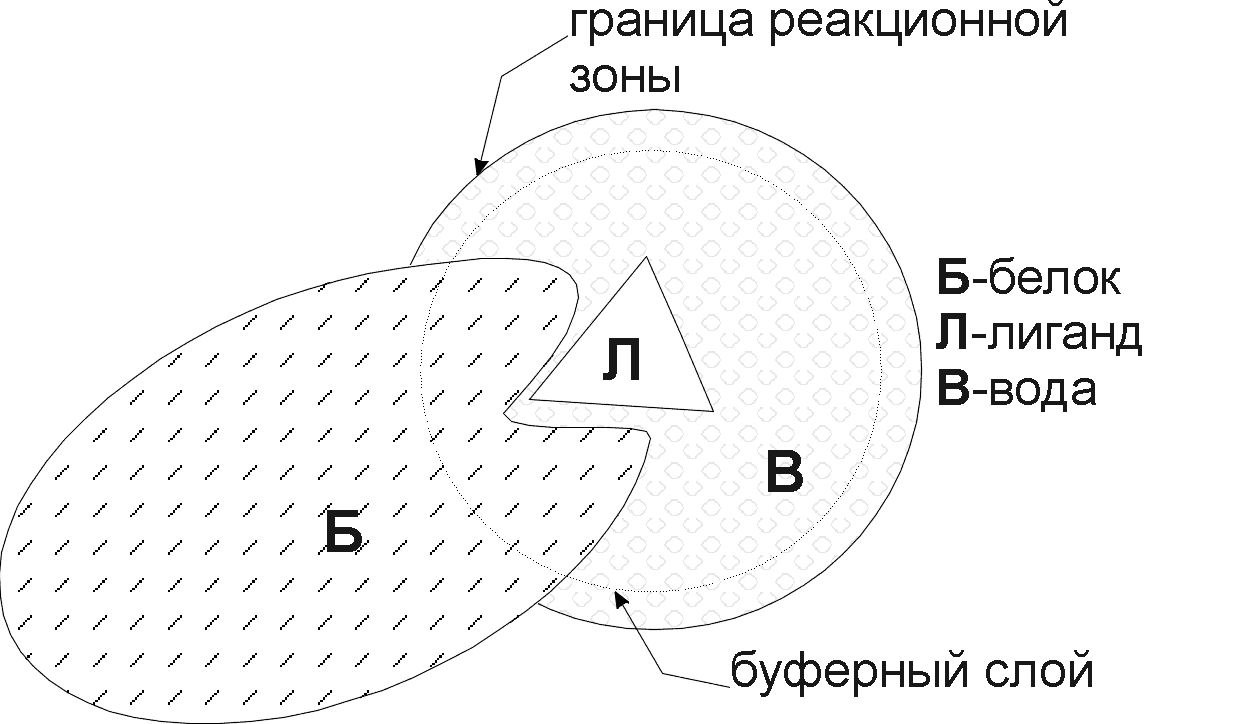
В качестве примера выбора средней силы рассмотрим процесс связывания лиганда. Выделение реакционной зоны в системе белок-лиганд-вода показано схематически на рисунке. Реакционная зона – это сфера с центром в «активном центре» и радиусом R₀ (R₀^» 10-20 A). Обычно используется следующий критерий включения атомов белка в окрестности границы РЗ: если какой-либо атом остатка попадает в РЗ, то в неё включаются и все остальные атомы остатка.

Среднюю силу для атомов белка и атомов растворителя выбирают по-разному. Поскольку белок обладает хорошо определённой средней структурой, то его атомы как правило совершают локализованные движения вокруг средних положений. Поэтому в качестве выбирается гармоническая сила, привязывающая атомы к равновесным положениям.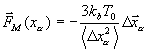

Эта сила действует на атомы белка только в буферной зоне. Здесь – среднеквадратичное уклонение атома. Для вычисления силы , действующей на атом растворителя, который находится в положении , со стороны всех остальных атомов резервуарной области, необходимо провести усреднение по равновесному распределению растворителя

Здесь есть сила взаимодействия между атомами растворителя, а – равновесная парная функция распределения.

В методе столкновительной динамики (СД) связь с тепловым резервуаром моделируется столкновением с виртуальными атомами резервуара. При этом, как и в методе Андерсона (МА), в некоторые моменты t_k происходит замена скоростей. Новые скорости вычисляются как результат столкновения системы с виртуальным атомом, имеющим массу m₀ и скорость . Скорость – случайная величина, которая берётся из распределения Максвелла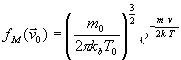

В промежутке между последовательными столкновениями, система движется в соответствии с уравнениями Гамильтона как и в традиционной молекулярной динамике. В методах СД и МА моменты времени t_k, в которые происходит замена скоростей (далее – моменты столкновений), суть случайные величины, образующие пуассоновский поток событий. Это означает следующее.

а) Вероятность того, что на интервале времени [0,t] произойдёт ровно n столкновений, равна

б) Интервалы времени между последовательными столкновениями суть независимые случайные величины, распределённые по Пуассону

Исходя из этого, величина l имеет смысл среднего количества столкновений в единицу времени (частота столкновений), а величина имеет смысл среднего интервала времени.

Поведение траекторий, моделируемое МА и СД, в фазовом пространстве системы, следующее. Некоторое случайное время траектория движется в соответствии с динамическими уравнениями по поверхности постоянных энергий и импульса П_k. Затем, она мгновенно перепрыгивает на другую поверхность П_k+1, по которой движется случайное время и т. д. Причём скачок происходит только в импульсной части фазового пространства. Координаты и, следовательно, потенциальная энергия остаются во время скачка неизменными.

Отличие методов состоит в том, как осуществляется этот скачок скоростей. В МА новые скорости выбираются независимо от того, какие скорости были до скачка. При этом средняя величина скачка не регулируется и постоянна (при постоянной температуре). В СД выбор новых скоростей зависит от того, из какой точки фазового пространства мы делаем скачок. Наличие такого параметра, как масса атомов резервуара, позволяет регулировать силу удара, испытываемого системой при столкновении, и, следовательно, влиять на динамику флуктуаций и релаксационные процессы.

Литература:

1. Berendsen H.J.C., Postma J.P.M., van Gunsteren W.F., DiNola A., Haak J.R. Molecular dinamics with coupling to an external bath,. J. Chem. Phys., 81, 3684-3690, 1984.
2. Andersen H.C. Molecular dynamics simulations at constant pressure and/or temperature, J. Chem. Phys., 72, 2384-2393, 1980.
   32. Kuharski R.A., Candler D., Montgomery J.A., Rabii F., Singer S. J. Stochastic molecular dynamics study of cyclohexane isomerisation., J. Phys. Chem., 92, 3261-3267, 1988.
3. Nose S. A molecular dynamics method for simulations in the canonical ensemble., Molec. Phys., 52, 255-268, 1984.
4. Bercowitz M., McCammon J.A. Molecular dynamics with stochastic boundary conditions, Chem. Phys. Lett., 90, 215-217, 1982.
5. Brooks III C.L., Brunger A., Karplus M. Active site dynamics: A stochastic boundary MD approach., Biopolymers, 24, 843, 1985.
6. Brooks C.L., Karplus M. Solvent effects on protein motion and protein effects on solvent motion. Dynamics of the active site region of lisozyme., J. Mol. Biol., 208, 159-181, 1989.
7. Brunger A., Brooks III C.L., Karplus M. Active site dynamics of ribonuclease., Proc. Natl. Acad. Sci. USA, 82, 8458-8462, 1985.

<< Назад || Вперёд >>

Обратно в оглавление